Introducción

Las variedades surgen de muchas maneras. En análisis complejo las variedades aparecen como el espacio en el que están “naturalmente” definidas ciertas funciones, en ecuaciones diferenciales ocurren como espacios de configuraciones, en mecánica emergen de las restricciones holonómicas del movimiento. Sin embargo hay una visión que en cierto modo subyace todas las anteriores y que además tiene la ventaja de ser filosóficamente interesante.

Quizá la mejor manera de introducir el concepto de variedad sería señalando la larga historia a lo largo de la cual los seres humanos han intentado racionalizar y estructurar el espacio que habitamos. Y es que ofrece una buena analogía con muchos de los conceptos básicos de la topología y geometría diferencial. Así que sugiero que el lector se ponga en la siguiente situación:

Habría que olvidar un poco que vivimos en un espacio casi plano, o incluso que la tierra es una gran esfera, y en cambio remontarnos a un hipotético pasado previo a los mapas y la navegación. Y para hacer el escenario completamente irreal supongamos también que por suerte se han desarrollado las herramientas del cálculo. En tal situación lo natural sería hacer lo que cualquier cartógrafo amateur haría, tomar un pedazo de hilo, o un palo, como estándar, y empezar a dibujar una cuadrícula alrededor de uno mismo. O quizá ni siquiera habría necesidad de cuantificar el espacio de un modo rígido, a veces un obstáculo o algún rasgo particular del espacio nos obligaría a tomar coordenadas “curvas”. Sin embargo el mero hecho de asignarle a cada punto del espacio n números o coordenadas (la idea vaga a la cual aludió Bernhard Riemman) resulta ya una idea extravagante y poderosa. Así los objetos y los fenómenos físicos pueden ser descritos con funciones, superficies, y demás objetos analizables con el cálculo.

De este modo, al poner coordenadas en un espacio extraño y desconocido, hemos transformado al espacio en un objeto conocido y manso. Una transformación que a los objetos concretos del espacio los representa en el lenguaje de $\mathbb{R}^n$ y el cálculo.

Nadie dijo que fuera posible, y quizá para la realidad en que vivimos sólo es un modelo un tanto impreciso. Esto es un problema filosófico de importancia, pero ya nos gustó la idea y de ahora en adelante haremos la trampa del matemático de enfocarse únicamente en los espacios que admiten semejante análisis. Estos espacios en los cuales se pueden introducir coordenadas son llamados variedades y son el punto de partida no sólo de la geometría riemanniana, sino de abundantes ramas de la matemática y física. En lo que sigue haremos formal la idea vaga a la que hemos llegado aquí.

Definiciones

Todo comienza con poner coordenadas:

Una carta (o mapa) n-dimensional en un espacio topológico $X$ consta de la siguiente información:

Un abierto $U \subset X$.
Una función $\varphi_U: U \rightarrow V \subset \mathbb{R}^n$.

Donde $V$ es un abierto y $\varphi$ es un función continua con inversa continua. Dicho de otro modo $\varphi$ es un homeomorfismo. Diremos que $(U,\varphi_U)$ es una carta n-dimensional de $X$ si satisface las propiedades mencionadas. Las funciones inversas $\varphi_U^{-1}$ son llamadas parametrizaciones puesto que se piensa que se está "parametrizando" puntos de $X$ con $n$ números distintos.

Al tener una carta de una porción del espacio en cuestión, es posible comenzar con el análisis local usando las herramientas del cálculo. Las coordenadas proveen una manera de describir funciones en el espacio abstracto como si fueran funciones en $\mathbb{R}^n$. Sin embargo hay que tener cuidado: las propiedades de los objetos representados pueden depender de la carta usada para representarlos. En particular si estámos hablando de utilizar el cálculo como herramienta de descripción y análisis habría que tener cuidado de usar cartas que preserven la propiedad de diferenciabilidad. Explícitamente, si una función representada en una carta es diferenciable, preferiríamos que lo fuera también con cualquier otra carta.

Si $(U, \varphi_U)$ y $(V, \varphi_V)$ son un par de cartas n-dimensionales de $X$ y $U \cap V \neq \emptyset$ entonces la función $\psi_U^V: \varphi_U(U \cap V) \rightarrow \varphi_V(U \cap V)$ dada por $$ \psi_U^V = \varphi_V \circ \varphi_U^{-1} $$ es llamada función de cambio de coordenadas. Usaremos la notación $\varphi_U^V: (U, \varphi_U) \rightarrow (V, \varphi_V)$ para resumir esta información.

Noten que $\psi_U^V$ es una función que va de un abierto $\varphi_U(U \cap V) \subset \mathbb{R}^n$ de $\mathbb{R}^n$ en otro abierto $\varphi_V(U \cap V) \subset \mathbb{R}^n$ de $\mathbb{R}^n$. Es importante notar que la función de cambio de coordenadas sólo está definida en las porciones de espacio representado que corresponde con el espacio común a ambas cartas, es decir $U \cap V$.

Decimos que dos cartas n-dimensionales $(U, \varphi_U)$ y $(V, \varphi_V)$ son $C^r$ compatibles si $U \cap V = \emptyset$ o bien la función de cambio de coordenadas $\psi_U^V: (U, \varphi_U) \rightarrow (V, \varphi_V)$ es de tipo $C^r$.

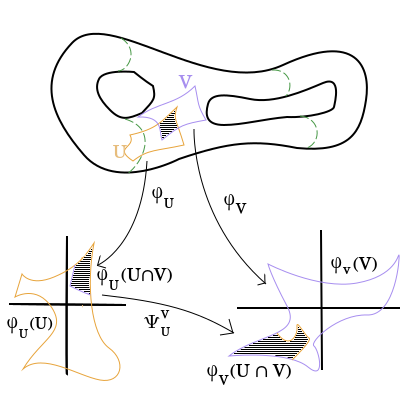
Recordamos que una función $g: U \subset \mathbb{R}^n \rightarrow \mathbb{R}^m$ es de tipo $C^r$ si todas las derivadas parciales de orden $r$ existen y son continuas.

Así hemos llegado a la definición correcta de los espacios que caerán bajo nuestro análisis. Son espacios abstractos en los cuales se puede usar las herramientas de cálculo, al menos de modo local (en pequeños pedazos), de modo consistente.

Un atlas $n$-dimensional (de tipo $C^r$) de $M$ es una colección de cartas $\mathcal{A} = \left\{ (U, \varphi_U) \mid U \in A \right\}$ n-dimensionales tales que

Todo par de cartas de $\mathcal{A}$ son $C^r$-compatibles.
Las cartas cubren a $M$, o dicho de otro modo, todo punto de $M$ está en una carta. Simbólicamente: $$ \bigcup_{(U,\varphi_U) \in \mathcal{A}} U = M $$

Si definieramos una variedad como un espacio topológico en el cual es posible definir un atlas surgiría una sutileza fundacional. Considerar dos variedades distintas únicamente por el hecho de que posiblemente un atlas tenga una carta más, sería tomar una noción de igualdad demasiado restrictiva. No es muy relevante el hecho de que, después de haber cubierto el espacio con mapas compatibles, se pueda encontrar una nueva carta, puesto que, en cierto modo, la “estructura diferenciable” ya está determinada por las primeras cartas. Para formalizar esta idea introducimos la siguiente noción:

Un atlas $\mathcal{A}$ de $M$ es maximal si toda carta $(U,\varphi_U)$ de $M$ que es compatible con las cartas de $\mathcal{A}$ está en $\mathcal{A}$. Dicho de otro modo, si $(U, \varphi_U)$ es tal que $(U, \varphi_U)$ es compatible con $(V, \varphi_V)$ para todo $(V, \varphi_V) \in \mathcal{A}$, entonces $(U, \varphi_U) \in \mathcal{A}$.

Sea $\mathcal{A}$ un altas de $M$.

Si $\mathcal{B}$ y $\mathcal{C}$ son atlas maximales de $M$ con $\mathcal{A} \subset \mathcal{B}, \mathcal{C}$ entonces $\mathcal{B} = \mathcal{C}$.
Existe un único altas maximal $\mathcal{A}^*$ de $M$ tal que $\mathcal{A} \subset \mathcal{A}^*$.

Luego para evitar distinguir entre objetos que deseamos pensar como iguales definiremos una variedad como un espacio topológico junto con un atlas maximal.

Una n-variedad diferenciable de tipo $C^r$ es un espacio topológico $M$ junto con atlas maximal $\mathcal{A}$ de tipo $C^r$ tal que

El espacio $M$ es Hausdorff (todo par de puntos pueden ser separados por abiertos).
Basta una cantidad contable de cartas $(U, \varphi_U) \in \mathcal{A}$ para cubrir todo $M$.

Funciones diferenciables

Ahora que hemos definido formalmente el tipo de espacio en el que trabajaremos podemos empezar a definir los objetos dentro del espacio que serán relevantes a nuestro estudio. Del mismo modo en que exigimos “diferenciablilidad” en el espacio, ahora pediremos que las funciones de interes sean diferenciables.

Sea $f:M \rightarrow N$ una función continua entre variedades $M$ y $N$ (de tipo $C^k$), y sea $p \in M$. Decimos que $f$ es diferenciable (de tipo $C^r$, con $r \leq k$) en $p$ si existen un par de cartas $(U, \varphi_U)$, $(V, \varphi_V)$, de $M$ y $N$ respectivamente, tales que

$p \in U$ y $f(p) \in V$.
La representación coordenada de $f$, dada por $\tilde f = \varphi_V \circ f \circ \varphi_U^{-1}$ (¿Donde está definida esta función?), es una función de tipo $C^r$ en $\varphi_U(p)$.

Aquí definimos la noción de diferenciabilidad con respecto a un par de cartas, sin embargo, podría suceder que si tomamos unas cartas ligeramente distintas la función que habíamos pensando diferenciable ya no lo es. La siguiente proposición prohibe que ocurra esto

Sea $f: M \rightarrow N$ una función diferenciable (de tipo $C^r$) en $p$. Si $(U',\varphi_{U'})$ y $(V', \varphi_{V'})$ son cartas cualesquiera con $p \in U'$ y $f(p) \in V'$, entonces la representación de $f$ en estas cartas $\hat f = \varphi_{V'} \circ f \circ \varphi_{U'}^{-1}$ es diferenciable (de tipo $C^r$) en $\varphi_{U'}(p)$.

Dado que $f$ es diferenciable en $p$ existen cartas $(U, \varphi_U)$ y $(V, \varphi_V)$ de $M$ y $N$ respectivamente con $p \in U$, $f(p) \in V$, y además son tales que la representación de $f$ en estas cartas $\tilde f = \varphi_V \circ f \circ \varphi_U^{-1}$ es diferenciable (de tipo $C^r$) en $\varphi_U(p)$. Notemos que $$ \hat f = \varphi_{V'} \circ f \circ \varphi_{U'}^{-1} = (\varphi_{V'} \circ \varphi_{V}^{-1}) \circ (\varphi_V \circ f \circ \varphi_U^{-1}) \circ (\varphi_U \circ \varphi_{U'}^{-1}) $$ al menos cerca de $\varphi_U(p)$ [Ejercicio: La ecuación anterior carece de formalidad puesto que los dominios de las funciones no siempre coinciden, ¿A que subconjuntos habría que restringirse para que la ecuación sea rigurosa?]. Así que $\hat f$ es la composición de tres funciones:

El cambio de coordenadas: $\Psi_{V}^{V'} = \varphi_{V'} \circ \varphi_{V}^{-1}$.
La representación de $f$: $\tilde f = (\varphi_V \circ f \circ \varphi_U^{-1})$.
El cambio de coordenadas: $\Psi_{U'}^{U} = \varphi_{U} \circ \varphi_{U'}^{-1}$

Las tres son funciones diferenciables (de tipo $C^r$), por lo que $\hat f$ es diferenciable en $\varphi_{U'}(p)$.

De este modo, podemos elegir la carta de nuestra preferencia para analizar el comportamiento de la función $f$ sin temor a perder la propiedad de diferenciabilidad.

Hay algunos tipos de funciones diferenciables que nos gustaría destacar

Una curva diferenciable es una función $\alpha: I \rightarrow M $ diferenciable, donde $I$ es algún intervalo abierto de $\mathbb{R}^n$.

Además de ser una descripción de un objeto geométrico 1-dimensional dentro el espacio, también se puede interpretar como un movimiento en la variedad. Es de este modo en que la dinámica se convierte en geometría, un lazo muy profundo y fértil del cual hablaremos más adelante.

Puesto que $\mathbb{R}^n$ es una variedad (como se verá en la sección de ejemplos) y es posible elegir las cartas de modo arbitrario, el hecho de que una función $f: M \rightarrow \mathbb{R}^n$ sea diferenciable se traduce a lo siguiente

Una función $f:M \rightarrow \mathbb{R}^n$ es diferenciable si para todo $p \in M$ existe una carta $(U, \varphi_U)$ cerca de $p$ tal que $$ \tilde f = f \circ \varphi_{U}^{-1} $$ es diferenciable.

Ejercicio

Finalmente, es de gran importancia, ya que se ha definido el concepto básico de la teoría en cuestión (que por el momento es la topología diferencial), definir también cual es la noción de equivalencia que se va a utilizar. O dicho de otro modo, se tiene que responder a la pregunta: para un topólogo diferencial, ¿qué quiere decir que dos objetos sean “iguales” o “equivalentes”?

Es filosóficamente equivalente al tratamiento que dan los fundacionistas de las matemáticas a los números. Para ellos, un número no un conjunto en particular, sino una propiedad que comparten todos los conjuntos biyectables entre si, y de hecho definida por esta noción de equivalencia.

La noción que han dado los topólogos diferenciales es la de difeomorfismo

Una función $f: M \rightarrow N$ es un difeomorfismo si $f$ es diferenciable, invertible y $f^{-1}$ es diferenciable. Si existe un difeomorfismo entre dos variedades $M$ y $N$, decimos que $M$ y $N$ son difeomorfas, y lo resumimos con el símbolo $M \cong N$.

Estructuras diferenciables

Esta sección es opcional, pero interesante.

Hemos definido la noción de una variedad diferenciable como un espacio en el cual se pueden encontrar cartas que sean compatibles entre si. Pero, ¿y si no nos interesa la diferenciabilidad? Podemos hablar de los espacios que admiten coordenadas sin exigir la compatibilidad:

Una variedad topológica es un espacio topológico $X$ tal que:

$X$ es Hausdorff.
$X$ es 2-numerable.
Para todo $p \in X$ existe una vecindad abierta $U \subset X$ de $p$ junto con un homeomorfismo $\varphi: U \rightarrow V \subset \mathbb{R}^n$ a un abierto $V \subset \mathbb{R}^n$. Un homeomorfismo es una función continua con inversa continua (la equivalencia del topólogo).

Por mucho tiempo los matemáticos no sabían si había alguna diferencia fundamental entre la definición de variedad topológica y variedad diferenciable. La pregunta que se sugería: ¿Toda variedad topológica es una variedad diferenciable? o dicho de otro modo ¿Si es posible poner coordenadas en un espacio, eso implica que es posible hacerlo de modo que los cambios de coordenadas sean diferenciables?. Y una segunda pregunta: ¿Y si es posible, de cuantas maneras no equivalentes se puede hacer?

Se dice que una variedad topológica $X$ es suavizable si existe un atlas $\mathscr{A}$ de tipo $C^r$ en $X$, con $r \geq 1$.

Existen variedades topológicas no suavizables (al menos dimensión $\geq 4$). Y son muchas.

Existen variedades topológicas que son suavizables de maneras esencialmente distintas. Esto es existen pares de variedades diferenciables $M$ y $N$ que son \it{homeomorfas} pero no \it{difeomorfas}. De nuevo esto sólo ocurre en dimensión $\geq 4$. En particular las esferas $\mathbb{S}^n$ tienen una cantidad finita de estructuras diferenciales distintas (admiten atlas no difeomorfos). Les dejamos una lista de la cantidad de estructuras diferenciales distintas en la esfera:

dim.	4	5	6	7	8	9	10	11	12	13	14	15
# est. dif.	??	1	1	28	2	8	6	992	1	3	2	16256

Para dimensión $4$ no se sabe casi nada. Y para añadir a su rareza:

Para $n \neq 4$ el espacio plano $\mathbb{R}^n$ tiene sólo una estructura diferenciable. Por otro lado $\mathbb{R}^4$ tiene una cantidad no numerable de estructuras diferenciables distintas.

Algunas de las herramientas utilizadas para demostrar estos teoremas usan de un modo clave el lenguaje de la geometría riemanniana y son temas de investigación actuales.

Ejemplos

Iremos desarrollando muchos ejemplos a lo largo del curso pero aquí hacemos explícitos los más sencillos.

La variedad más sencilla (salvo por los comentarios de la sección anterior) es $\mathbb{R}^n$. En este caso hay una carta, llamada la carta trivial, que cada punto funciona como su representación en coordenadas. Esto es $(\mathbb{R}^n,Id)$ (donde $Id(x) = x$) es una carta que cubre a todo $\mathbb{R}^n$. Tomando el atlas maximal que contiene a este se obtiene una estructura diferenciable en $\mathbb{R}^n$.

Sea $f: U \subset \mathbb{R}^n \rightarrow \mathbb{R}$ una función de tipo $C^1$. La gráfica de $f$, $$ Graf(f) = \left\{ (x,f(x)) \mid x \in U \right\} $$ es una variedad de dimensión $n$. De hecho, como $\mathbb{R}^n$, tiene una carta que la cubre por completo, a saber $(Graf(f), \pi)$, donde $\pi:\mathbb{R}^{n+1} \rightarrow \mathbb{R}^n$ es la función dada por $\pi(x_1,\cdots,x_n,x_{n+1}) = \left( x_1,\cdots,x_n \right)$.

La esfera n-dimensional $\mathbb{S}^n$, definida por $$ \mathbb{S}^n = \left\{ x \in \mathbb{R}^{n+1} \mid \|x\| = 1 \right\} $$ En particular $\mathbb{S}^2$ la esfera habitual, a la que reconocemos como la superficie en la que estamos destinados a vivir, es una variedad. La demostración de este hecho suele hacerse de dos maneras.

Dando cartas explícitas: Y para estas hay muchas de donde elegir. Basta con recurrir a la antiguísima ciencia de la cartografía para encontrar algunas: Un par de cartas que cubren a $\mathbb{S}^n$ hacen uso de la proyección estereográfica. La proyección estereográfica de la esféra $\mathbb{S}$ a $\mathbb{R}^n$ en el polo norte $N = (1,0,\cdots,0)$ esta dada por $$ \varphi_{N}(x,z) = \frac{1}{1-z} x $$ donde $(x,z) \in \mathbb{R}^{n+1} = \mathbb{R}^n \times \mathbb{R}$. Y la proyección estereográfica desde el polo sur, $S = (-1,0,\cdots,0)$, está dada por $$ \varphi_{S}(x,z) = \frac{1}{1+z} x $$ Es importante notar que estas dos funciones están definidas en $\mathbb{S}^n \setminus N$ y $\mathbb{S}^n \setminus S$, y luego ofrecen representaciones coordenadas distintas para los puntos en $\mathbb{S}^n \setminus \left\{ S,N \right\}$. Para estudiar la función de cambio de coordenadas notemos que $$ \varphi_S^{-1}(y) = \left(\frac{2y}{1+\| y\|^2}, \frac{1 - \|y \|^2}{1 + \|y\|^2}\right) $$ por lo que la función de cambio de coordenadas está dada por $$ \begin{aligned} \Phi_S^N(y) & = \varphi_N\left( \frac{2}{1 + \| y\|^2}y, \frac{1 - \| y \|^2}{1 + \| y\|^2} \right) \\ & =\frac{1 + \|y\|^2}{ 1- \|y\|^2} \frac{2}{1 + \|y \|^2}y \\ & = \frac{2}{1 - \| y\|^2}y \end{aligned} $$ y es diferenciable en $\mathbb{R}^n \setminus 0$. Con este atlas se le puede dar una estructura de variedad diferenciable a $\mathbb{S}^n$. Esta estructura de la esfera es llamada la canónica (puesto que ya vimos en la sección pasada que pueden existir varias).
Una segunda manera de demostrar que $\mathbb{S}^n$ es una variedad es usando el hecho de que $\mathbb{S}^n = f^{-1}(0)$ donde $f:\mathbb{R}^{n+1} \rightarrow \mathbb{R}$ es la función diferenciable dada por $f(x) = \| x\|^2 -1$. Esta función resulta ser regular (concepto que definiremos más adelante) en todos los puntos de $\mathbb{S}^n$ lo cual garantiza que $\mathbb{S}^n$ sea una variedad.