Notas de Subvariedades

versión pdf

Introducción

La geometría diferencial no comenzó tratando espacios abstractos sino una familia particular de objetos hoy llamados subvariedades. Son el tipo de objetos con los que interactuamos cotidaneamente: superficies, curvas, cuerpos sólidos. Todos estos son subconjuntos de un espacio que asumimos planos, es decir $\mathbb{R}^3$. Sin embargo no todos los subconjuntos de $\mathbb{R}^3$ son lo suficientemente decentes como para poder ser analizables con cálculo. La propiedad que separa las subvariedades de los demás subconjuntos es el hecho de poseer planos (o lineas) tangentes. Esto asegura que la superficie (o curva) es suficientemente suave como para poder describirla correctamente con funciones diferenciables.

Subvariedades Inmersas

Recordemos que

Una parametrización en $\mathbb{R}^n$ es una función diferenciable $\varphi: U \subset \mathbb{R}^k \rightarrow \mathbb{R}^n$.

Las parametrizaciones pueden ser utilizadas para describir el subconjunto $\varphi(U)$ con la ayuda de $k$-parámetros. Sin embargo algunas parametrizaciones sufren de “singularidades” o puntos donde la diferencial es singular. Esto puede introducir esquinas o aberraciones más graves en la forma que los parámetros describen al conjunto $\varphi(U)$.

Para evitar este comportamiento basta con pedir que la diferencial tenga rango máximo. En este caso, si $k < n$, el teorema de la inmersión nos dice que, salvo cambios de coordenadas en el codominio, la parametrización es identica a meter un pedazo de plano $k$-dimensional en $\mathbb{R}^n$. Y, dado que los cambios de coordenada son diferenciables, dicho pedazo, visto en las coordenadas normales, es “suave” y similar a un plano (al verlo de cerca).

Una parametrización $f: U \subset \mathbb{R}^k \rightarrow \mathbb{R}^n$ es una inmersión si para todo $p \in U$ la diferencial $Df_p$ es inyectiva (o de rango máximo).

Las superficies, o en general las subvariedades, son subespacios que son descriptibles con parametrizaciones

Un subconjunto $A \subset \mathbb{R}^n$ es una subvariedad inmersa de dimensión $k$ (de tipo $C^r$) si existe una cantidad contable de inmersiones $\varphi_{\alpha}: U_{\alpha} \subset \mathbb{R}^k \rightarrow \mathbb{R}^n$ (de tipo $C^r$) con $\alpha \in \mathcal{A}$ tal que $$ A = \bigcup_{\alpha \in \mathcal{A}} \varphi_{\alpha}(U_{\alpha}) $$

Notemos que la definición de subvariedad inmersa no exige que las parametrizaciones sean inyectivas. Una curva que se autointersecta, pero que siempre tiene vector tangente no nulo, es una subvariedad de dimensión uno.

Otro ejemplo un poco más extraño lo brinda la botella de klein

que se autointersecta en un círculo. Cerca de los puntos de autointersección la superficie se ve como dos planos intersectandose en una linea.

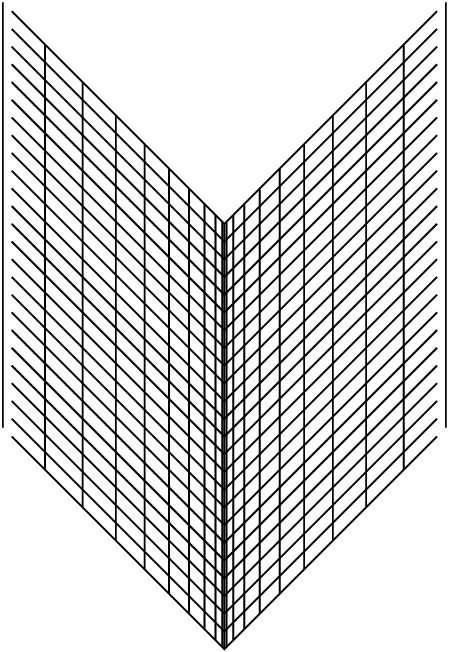
Otra posibilidad sería como en la siguiente figura

que está formada por una curva que se enrolla hasta una curva límite y la curva límite. Tanto la espiral como la curva límite se pueden describir como imagenes de inmersiones de $\mathbb{R}^1$ en $\mathbb{R}^2$. Si se enfocan en un punto en la espiral, basta con acercarse lo suficiente para que el conjunto parezca una linea cruzando el plano. Sin embargo esto deja de ser cierto en los puntos sobre la curva límite. En dichos puntos, no importa que tanto se acerce uno siempre seguirán apareciendo una cantidad infinita de lineas que se aproximan al punto.

Recordemos que si $X$ es un espacio topológico y $A \subset X$ es un subconjunto, entonces $A$ hereda una topología de $X$ en la cual los abiertos de $A$ son del tipo $U \cap A$, con $U$ abierto de $X$. Esta es llamada la topología de subespacio. Si a una subvariedad inmersa le damos la topología de subespacio que hereda de $\mathbb{R}^n$ entonces hemos visto un par de ejemplos en los cuales existen puntos con vecindades del tipo:

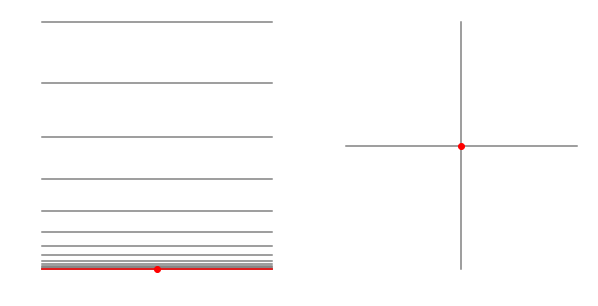
Estas vecindades no son ni siquiera homeomorfas a abiertos de $\mathbb{R}^n$ por lo que, en general, las subvariedades inmersas no son variedades. Al menos si uno usa la topología de subespacio. Entonces, ¿por qué reciben ese nombre?

Una función diferenciable $f: N \rightarrow M$, entre variedades diferenciables $N$ y $M$, es una inmersión si para todo $p \in N$ existe una representación coordenada de $f$ alrededor de $p$, digamos $\tilde f$, tal que $\tilde f: U \subset \mathbb{R}^n \rightarrow \mathbb{R}^m$ es una inmersión.

Aunque la definición de la propiedad de inmersión depende de el uso de representaciones coordenadas específicas es posible ver que no depende de la representación elegida.

Si $f: N \rightarrow M$ es una inmersión y $\tilde f$ es cualquier representación coordenada de $f$ entonces $\tilde f$ es una inmersión.

Sean $(U, \varphi_U)$ y $(V, \varphi_V)$ cartas alrededor de $p \in N$ y $f(p) \in M$. La representación definida por estas cartas sólo está definida cuando todas los objetos involucrados caen dentro de las descripciones coordenadas de $U$ y $V$. Por ejemplo, si $q \in U$ es tal que $f(q) \notin V$, entonces es imposible representar a $f(q)$ en términos de las coordenadas brindadas por $\varphi_V$. Así que es necesario restringirse primero a $W = f^{-1}(V) \cap U$. Por suerte $p \in W$. Luego la representación coordenada $\tilde f = \varphi_V \circ f \circ \varphi_U^{-1}$ sólamente está definida en $\varphi_{U}(W)$. Ya que hemos arreglado la cuestión del dominio, hemos de ver que en efecto $\tilde f$ es una inmersión, o bien que para todo $y \in \varphi_U(W)$ la diferencial $D \tilde f_y$ es inyectiva. Sea $y \in \varphi_U(W)$ y $q = \varphi_U^{-1}(y)$. Por la definición de inmersión existen un par de cartas $(U',\varphi_{U'})$ y $(V', \varphi_{V'})$ alrededor de $q$ y $f(q)$ tal que la representación coordenada $\bar f = \varphi_{V'} \circ f \circ \varphi_{U'}^{-1}$ es una inmersión, en particular si $y' = \varphi_{U'}(q)$ entonces $D \bar f_{y'}$ es inyectiva. De nuevo la representación coordenada $\bar f$ sólo está definida en $\varphi_{U'}( U' \cap f^{-1}(V'))$. Tenemos dos representaciones coordenadas, y estas diferen por un cambio de coordenadas $$ \begin{aligned} \tilde f & = \varphi_{V} \circ f \circ \varphi_{U}^{-1} \\ & = \varphi_{V} \circ \varphi_{V'}^{-1} \circ \varphi_{V'} \circ f \circ \varphi_{U'}^{-1} \circ \varphi_{U'} \circ \varphi_{U}^{-1} \\ & = \Psi_{V'}^V \circ \bar f \circ \Psi_{U}^{U'} \end{aligned} $$ Para que esto funcione hay que cuadrar los dominios. Lo importante es que $y$ cae dentro del dominio en el cual la ecuación anterior es válida [Ejercicio: ¿Por qué?]. Simplifiquemos un poco la notación: $x = \varphi_V(f(q))$ y $x' = \varphi_{V'}(f(q))$, por lo que $\bar f(y') = x'$ y $\tilde f(y) = x$. 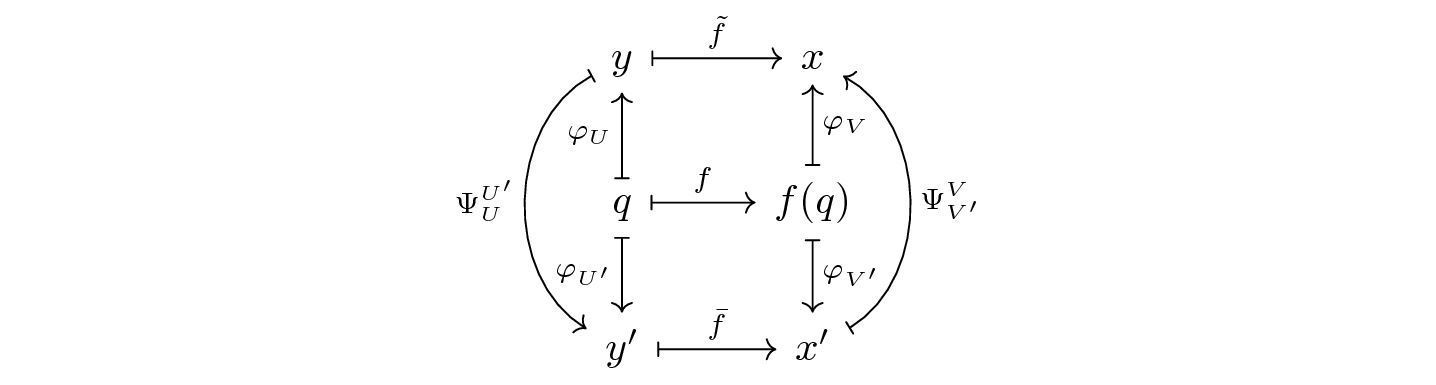Dado que los cambios de coordenadas son difeomorfismos en particular sus diferenciales son inyectivas en todo punto, y por la regla de la cadena $$ D \tilde f_y = D(\Psi_{V'}^V)_{x'} \circ D\bar f_{y'} \circ D(\Psi_{U}^{U'})_{y} $$ Así $D \tilde f_y$ es una composición de transformaciones lineales inyectivas y por lo tanto inyectiva ella misma.

Más adelante daremos una descripcióń de inmersión que no depende del uso de coordenadas, pero será hasta que desarrollemos el lenguaje de los vectores tangentes.

Resulta que toda subvariedad inmersa de $\mathbb{R}^n$ es realmente la imagen de una inmersión $f: N \rightarrow \mathbb{R}^n$. Luego podemos extender la definición de subvariedad inmersa de $\mathbb{R}^n$ a cualquier variedad.

Nueva definición de subvariedad inmersa: Si $M$ es una variedad diferenciable entonces $A \subset M$ es una subvariedad inmersa de dimensión $k$ (y tipo $C^r$) si existe una variedad $N$ (de tipo $C^k$ con $k \geq r$) y una inmersión $f: N \rightarrow M$ (de tipo $C^r$) tal que $A = f(N)$.

Lo que mencionamos anteriormente se puede resumir en lo siguiente: Si $f: N \rightarrow \mathbb{R}^n$ es una inmersión entonces $f(N)$ como subespacio de $\mathbb{R}^n$ puede no tener la misma topología que $N$. Para esto presentamos el concepto de encaje

Una función $f: X \rightarrow Y$ es un encaje si $f$ es continua, inyectiva y $f^{-1}$ es continua en $f(X)$ cuando se le dota a $f(X)$ la topología de subespacio. Esto es $X$ y $f(X)$ son homeomorfos a través de $f$.

Subvariedades encajadas

Podríamos definir subvariedad encajada usando la definición anterior:

Un subconjunto $A \subset M$ es una subvariedad encajada si existe una variedad $N$ junto con un encaje e inmersión $f: N \rightarrow M$ tal que $A = f(N)$. Sin embargo esta definición es un tanto impráctica al momento de demostrar que algo es una subvariedad encajada. Es por esto que damos la definición alternativa

Sea $M$ una variedad diferenciable n-dimensional y $A \subset M$. Decimos que $A$ es una subvariedad encajada de dimensión $m$ si para todo $p \in A$ existe una carta $(U, \varphi_U)$ alrededor de $p$ tal que $$ \varphi_U(A \cap U) \subset \mathbb{R}^m \times \left\{ 0 \right\} $$ es decir, existe un sistema coordenado alrededor de $p$ en el cual el pedazo de $A$ dentro de $U$ está descrito como un pedazo del subespacio $m$ dimensional de $\mathbb{R}^n$ dado por $$ \left\{ (x_1,\cdots,x_m,0,\cdots,0) \in \mid x_1,\cdots,x_n \in \mathbb{R} \right\} $$

La siguiente imagen representa el cambio de coordenadas del que habla la definición anterior:

Demostrar que la definición que se acaba de dar es lo mismo que la definición que mencionamos previamente requiere un poco de trabajo y se los dejamos como proyecto para este parcial.

Uno de los métodos más útiles para producir nuevas variedades, o demostrar que cierto subconjunto es una subvariedad encajada, es a través de las sumersiones.

Una función diferenciable $f: M \rightarrow N$ entre variedades diferenciables es una sumersión si para todo punto $p \in M$ existe una representación coordenada de $f$ alrededor de $p$, digamos $\tilde f$, tal que $D \tilde f_y$ es suprayectiva (o de rango máximo) para todo $y$ en el dominio de $\tilde f$.

De nuevo esta definición no depende de la representación coordenada elegida

Si $f$ es una sumersión y $\tilde f$ es cualquier representación coordenada de $f$ entonces $D \tilde f_y$ es suprayectiva para todo $y$ en el dominio de $\tilde f$.

Demuéstralo.

Las sumersiones tienen representaciones locales sencillas, salvo cambio de coordenadas son proyecciones, por lo que los conjuntos de nivel parecen, al menos localmente, subespacios de $\mathbb{R}^n$. Esto es justo la definición de subvariedad encajada:

Sea $f: M \rightarrow N$ una función diferenciable entre variedades de dimensión $m$ y $n$, respectivamente, con $m > n$ y $p \in M$ tal que $f(p) = y$ es un valor regular (i.e. para todo $q \in f^{-1}(y)$ la diferencial $Df_q$ es de rango máximo), entonces $A = f^{-1}(y)$ es una subvariedad encajada de $M$ de dimensión $m-n$.

Sea $q \in f^{-1}(y)$. Queremos demostrar que existe una carta $(U, \varphi_U)$ cerca de $q$ tal que $$ \varphi_U(A \cap U) \subset \mathbb{R}^{m-n} \times \left\{ 0 \right\} $$ Puesto que $f$ es una sumersión en $q$ (o bien $Df_q$ es suprayetiva) por hipótesis, por el teorema de la sumersión sabemos que podemos encontrar cartas $(U,\varphi_U)$ y $(V, \varphi_V)$ cerca de $q$ y $y = f(q)$ tales que $$ \varphi_V \circ f \circ \varphi_U^{-1}(x,y) = \tilde f(x,y) = y $$ con $(x,y) \in \mathbb{R}^{m-n} \times \mathbb{R}^n$. Notemos que si $\varphi_{U}(q) = (x',y')$ entonces cualquier punto de la forma $(x,y')$ satisface $\tilde f(x,y') = y' = \tilde f(x,y)$. Esto implica que $$ \left\{ (x,y') \mid x \in \mathbb{R}^{m-k} \right\} \cap Dom(\tilde f) = \varphi_U(A \cap U) \cap Dom(\tilde f) $$ Modificando el dominio de la carta a $U'$ y transladando de modo que $\varphi_{U'}(q) = (x', 0)$ obtenemos una carta $(U', \varphi_{U'})$ cerca de $q$ tal que $$ \varphi_{U'}(A \cap U') \subset \mathbb{R}^{m-n} \times \left\{ 0 \right\} $$