Encontré estas notas de particiones de la unidad que hicimos hace unos años para los alumnos de cálculo iv. Espero que les sean de utilidad.
Introducción
Las particiones de la unidad son una herramienta fundamental en diversas areas del análisis y la geometría. Su importancia radica en que su uso permite construir objetos “globales” a partir de objetos “locales”, o demostrar la validez de una propiedad “globalmente” a partir de su validez “local”. Aunque lo dicho hasta ahora ha sido bastante ambiguo, el uso repetido de las particiones de la unidad proverá la intuición y justificación suficiente para entender lo que se quiso decir con el enunciado pasado. Dado que las propiedades y los objetos que nos preocupan son diferenciables, buscamos que la construcción del objeto “global” también sea diferenciable.
Dado que no hemos encontrado una manera satisfactoria de motivar las particiones de la unidad (sin ser demasiado circulares) entraremos en materia sin preludios.
Funciones características suaves
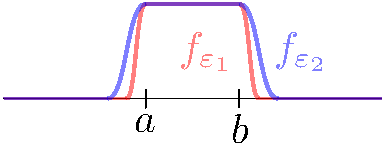
Sea $[a,b] \subset \mathbb{R}$ un intevalo. La función característica $\chi=\chi_{[a,b]}$ sufre un cambio súbito en la frontera de $[a,b]$ por lo que $\chi$ no es una función continua (y mucho menos diferenciable). En esta sección construiremos una familia de funciones $f_{\varepsilon}: \mathbb{R} \rightarrow \mathbb{R}$ infinitamente diferenciables que satisfagan algo parecido a $\chi$, a saber $f_{\varepsilon}(x) = 1$ si $x \in [a,b]$ y $f_{\varepsilon}(x) = 0$ si $d(x,[a,b]) \geq \varepsilon$, con la propiedad extra de ser nunca negativa, i.e. $f_{\varepsilon}(y) \geq 0$ para todo $y \in \mathbb{R}$. Nótese que la condición $d(x,[a,b])$ es equivalente a $x \geq b + \varepsilon$ o $x \leq a - \varepsilon$. La figura esboza las funciones $f_{\varepsilon}$.
Para esto consideremos la siguiente función Ponemos aquí su gráfica:
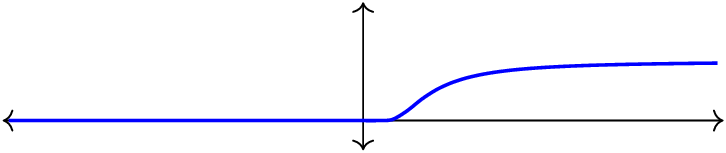
Notemos un par de cosas: En primer lugar si $x \to \infty$ entonces $x^2 \to \infty$ y por lo tanto $\frac{1}{x^2} \to 0$. Luego $e^{1/x^2} \to 1$ y finalmente
Por otro lado cuando $x \to 0^+$ entonces $\frac{1}{x^2} \to \infty$ y por lo tanto $\frac{1}{e^{(1/x^2)}} \to 0$. Es decir y por lo tanto $F$ es continua.
La función $F$ es de clase $C^{\infty}$.
Dado que la demostración es de naturaleza técnica la dejamos para un apéndice.
La función $F$ satisface tres propiedades: $F$ es $C^{\infty}$, $F(x) = 0$ si y solo si $x \leq 0$ y $F(x) \geq 0$ para toda $x \in \mathbb{R}$. Para lo que sigue podemos utilizar cualquier función $F$ que satisfaga estas condiciones, bastenos con saber que existe al menos una.
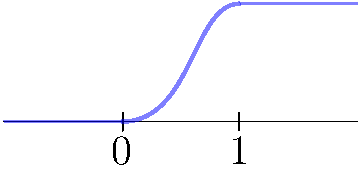
Definamos $G: \mathbb{R} \rightarrow \mathbb{R} $ como $G(x) = F(x)F(1-x) $. Esta función es $C^{\infty}$ y satisface que $G(x) = 0$ si y solo si $x \notin (0,1)$ y que $G(x) \geq 0$ para toda $x \in \mathbb{R}$. Finalmente sea $H(x) = \frac{\int_0^x G(x)}{\int_0^1 G(x)}$.
$H$ es una función $C^{\infty}$ tal que
- $H(x) = 0$ para $x \leq 0$.
- $H(x) = 1$ para $x \geq 1$.
- $H(x) \geq 0$ para toda $x \in \mathbb{R}$.
$H$ es $C^{\infty}$ ya que $H' = G$ y $G$ es $C^{\infty}$. Sea $x \leq 0$. Nótese que $G$ es $0$ en el intervalo $[x,0]$ y por lo tanto $H(x)= \int_0^x G / \int_0^1 G = 0$.
Si $x \geq 1$ entonces $G$ es $0$ en el intervalo $[1,x]$. Consecuentemente $\int_1^x G = 0$ y luego $H(x) = \int_0^x G / \int_0^1G = (\int_0^1 G +\int_1^x G)/(\int_0^1 G) = 1$.
Para $x \in (0,1)$, $G(x) \geq 0$ y por lo tanto $\int_0^1 G > 0$ y $H(x) = \int_0^x G / \int_0^1 G \geq 0$.
Con estas funciones construiremos el objeto deseado.
Sean $a\leq b \in \mathbb{R}$ y $\varepsilon>0$. Existe $g= g_{[a,b]}^{\varepsilon} : \mathbb{R} \rightarrow \mathbb{R} $ función $C^{\infty}$ tal que $g(x) \geq 0$ para todo $x \in \mathbb{R}$,
$g(x) = 1$ si $x \in [a,b]$ y $g(x) = 0$ si $d(x,[a,b]) \geq \varepsilon$.
Sean $a\leq b$ y $\varepsilon>0$. Consideremos las funciones
$$
\begin{aligned}
h_a^{\varepsilon}(t) = H\left(\frac{t-(a-\varepsilon)}{\varepsilon} \right)\\
h_b^{\varepsilon}(t) = H\left(\frac{(b+\varepsilon) - t}{\varepsilon} \right)
\end{aligned}
$$
Nótese que $h_a^{\epsilon}(t) =0$ si $\frac{t-(a-\varepsilon)}{\varepsilon} \leq 0 $, es decir $t \leq a-\varepsilon$ y que $h_a^{\varepsilon}(t) = 1$
si $\frac{t - (a-\varepsilon)}{\varepsilon} \geq 1$, es decir $t \geq a$. Análogamente $h_{b}^{\varepsilon}(t) = 0$ para $x \in [b+\varepsilon,\infty)$
y $h_{b}^{\varepsilon}(t) = 1$ para $x \in (\infty,b]$. Además $h_a^{\varepsilon},h_b^{\varepsilon}$ son no negativas y $C^{\infty}$.
Definimos $g_{[a,b]}^{\varepsilon}(t) = h_a^{\varepsilon}(t)h_b^{\varepsilon}(t)$. El lector puede revisar que $g_{[a,b]}^{\varepsilon}$ satisface las propiedades deseadas.
Las funciones $g_{[a,b]}^{\varepsilon}$ son aproximaciones suaves ($C^{\infty}$) a la función característica de $[a,b]$, sin embargo no es la función característica de algún conjunto ya que toma otros valores aparte de $1$ y $0$ (¿por qué?). Si $\varepsilon_k$ es una sucesión de números positivos con $\varepsilon_k \to 0$ entonces no es muy dificil demostrar que donde la convegencia es puntual.
Demuestra esto.
Ahora queremos extender este resultado para rectángulos $R \subset \mathbb{R}^n$.
Sea $R = [a_1,b_1]\times...\times[a_n,b_n]\subset\mathbb{R}^n$ un rectángulo y $\varepsilon>0$. La $\varepsilon$-vecindad rectángular de $R$ es el conjunto
$R^\varepsilon = [a_1-\varepsilon,b_1+\varepsilon]\times...\times[a_n-\varepsilon,b_n+\varepsilon]$.
Sea $R = [a_1,b_1] \times ... \times [a_n,b_n] \subset \mathbb{R}^n$ un rectángulo y $\varepsilon>0$. Si $x \in R^{\varepsilon}$, demuestra que $d(x,R) \leq \sqrt{n}\varepsilon$.
Si $x = (x_1,...,x_n) \in \mathbb{R}^n$ usaremos $R_\varepsilon(x)$ para denotar el rectángulo $R_{\varepsilon}(x) = [x_1-\varepsilon,x_1+\varepsilon]\times...\times [x_n-\varepsilon,x_n+\varepsilon]$.
Sea $R = [a_1,b_1] \times ... \times [a_n,b_n] \subset \mathbb{R}^n$ un rectángulo y $\varepsilon>0$. Existe una función $g_R^{\varepsilon} : \mathbb{R}^n \rightarrow \mathbb{R}$ tal que
- $g_R^{\varepsilon}$ es de clase $C^{\infty}$.
- $g_R^{\varepsilon}(x) \geq 0$ para todo $x \in \mathbb{R}^n$.
- $g_R^{\varepsilon}(x) = 1$ si $x \in R$.
- $g_R^{\varepsilon}(x) = 0$ si $d(x,R) \geq \varepsilon$.
Sea $R=[a_1,b_1] \times ... \times [a_n,b_n] $ un rectángulo y $\varepsilon>0$. Para cada $i \in \left\{1,..,n \right\}$ sea
$h_i = g_{[a_i,b_i]}^{\frac{\varepsilon}{\sqrt{n}}}: \mathbb{R} \rightarrow \mathbb{R}$ la función dada por la proposición. Esto es $h_i$ es una función tal que:
- [a:]
- $h_i$ es de clase $C^{\infty}$.
- $h_i(t) \geq 0$ para todo $t \in \mathbb{R}$.
- $h_i(t) = 1$ si $x \in [a_i,b_i]$.
- $h_i(t) = 0$ si $d(t,[a_i,b_i]) \geq \frac{\varepsilon}{\sqrt{n}}$, lo cual es equivalente a $t \notin (a_i-\frac{\varepsilon}{\sqrt{n}},b_i+\frac{\varepsilon}{\sqrt{n}} )$.
Como consecuencia tenemos la importante propiedad:
Sea $C \subset \mathbb{R}^n$ un conjunto compacto y $U$ un abierto tal que $C \subset U$. Existe una función $f:\mathbb{R}^n \rightarrow \mathbb{R}$ de clase $C^{\infty}$
tal que $0 \leq f(x) \leq 1$ para todo $x \in \mathbb{R}^n$, $f(x) = 1$ para todo $x \in C$ y $f(x) = 0$ para todo $x \in \mathbb{R}^n \setminus V$ donde $V$ es un abierto con $\overline{V}$ compacto y $\overline{V} \subset U $.
Sea $x \in C$. Dado que $U$ es un abierto existe $\varepsilon_x>0$ tal que $R_{\varepsilon_x}(x) \subset U$. Sean $R_x = R_{\varepsilon_x/2}(x)$ y $U_x= int(W_x)$.
El conjunto $\left\{ U_x \right\}_{x \in C}$ forma una cubierta abierta de $C$. Por compacidad de $C$ existen $x_1,...,x_r$ tales que $\left\{ U_{x_1},...,U_{x_r} \right\}$ es
una cubierta de $C$. Para cada $i = 1,...,r$ sea $g_i = g_{R_{x_i}}^{\varepsilon_{x_i}/2}$ como en la proposición. Notemos que $g_i$ es una función $C^{\infty}$ tal que
$g_i(y) = 1$ para $y \in R_{x_i}$, $g_{i}(y) = 0$ para $y \in \mathbb{R}^n \setminus R_{\varepsilon}(x)$ y $g_i(y) \geq 0$ para toda $y \in \mathbb{R}^n$.
Consideremos la función $h(x) = \sum_{i = 1}^r g_i(x)$, noten que $h$ es $C^{\infty}$.
Sea $V = \bigcup_{i=1}^r int(R_{x_i})$. $V$ es la union finita de conjuntos compactos y consecuentemente compacto. Dado que $R_{\varepsilon_{x_i}}(x_i) \subset U$ para todo
$i = 1,...,n$ se tiene que $\overline{V} \subset U$. Si $x \notin V$ entonces $x \notin R_{\varepsilon_{x_i}}(x_{i})$ para toda $i=1,...,r$ y por lo tanto $h(x) = 0$.
Por otro lado si $x \in C$ entonces $x \in R_{x_i}$ para algún $i \in \left\{ 1,...,r \right\}$ y
por lo tanto
$$
h(x) = \sum_{j = 1}^r g_j(x) = g_i(x) + \sum_{j=1,j\neq i}^{r}g_j(x) \geq g_i(x) = 1
$$
Finalmente sea $f = H \circ h$, donde $H$ es la función de la proposición. Por ser composición de funciones $C^{\infty}$, $f$ es de clase $C^{\infty}$.
Si $x \in \mathbb{R}^n \setminus V$ entonces $h(x) = 0$ y por lo tanto $f(x)=H(h(x)) = 0$.
Por otro lado si $x \in C$ entonces $h(x) \geq 1$ y por lo tanto $f(x) = H(h(x)) = 1$. La primer propiedad es consecuencia de que $Im(H) = [0,1]$.
Dejamos algunos ejercicios relacionados.
Sea $R \subset \mathbb{R}^n$ un rectángulo y $\varepsilon_k$ una sucesión de números positivos tales que $\varepsilon_k \to 0$. Demuestra que $g_R^{\varepsilon_k} \to \chi_R$.
Una función $f: \mathbb{R} \rightarrow \mathbb{R}$ es una función analítica o de clase $C^{\omega}$ si es infinitamente diferenciable y además para todo $x \in \mathbb{R}$ existe una
vecindad abierta $U$ de $x$ tal que
$$
f(y) = \sum_{i=0}^{\infty} \frac{f^{(i)}}{i!} (y-x)^i
$$
para toda $y \in U$. Esto es $f$ coincide con su serie de Taylor en una vecindad de $x$.
Sea $f: \mathbb{R} \rightarrow \mathbb{R}$ una función analítica. Demuestra que si existe $U \subset \mathbb{R}$ abierto tal que $f(x) = 0$ para toda $x \in U$ entonces $f(x) = 0$ para
toda $x \in \mathbb{R}$. Concluye que no existe una función $C^{\omega}$ que satisfaga las propiedades de la proposición.
Sean $x \in \mathbb{R}$ y $\varepsilon_k$ una sucesión de números positivos tales que $\varepsilon_k \to 0$. Las funciones $g^k_x=g_{[x,x]}^{\varepsilon_k}$ solo valen $1$ en $x$ y valen
$0$ fuera de $(x-\varepsilon_k,x+\varepsilon_k)$. Sean $\varphi^k_x: \mathbb{R} \rightarrow \mathbb{R}$ las funciones definidas por
$$
\varphi^k_x(x) = \frac{g^k_x(x)}{\int_{-\infty}^{\infty}g^k_x}
$$
Demuestra que
- $\left\{ \varphi^k_x \right\}_{k \in \mathbb{N}}$ es una sucesión de funciónes $C^{\infty}$ tales que $\int_{-\infty}^{\infty} \varphi^k_x = 1$ y $\varphi^k_x(x) = 0$ para toda $x \notin B_{\varepsilon}(x)$.
- Sea $g : \mathbb{R} \rightarrow \mathbb{R}$ una función continua. Demuestra que $$ \lim_{k \to \infty} \int_{-\infty}^{\infty} \varphi^k_x g = g(x) $$
- Sea $\varphi_k = \varphi_0^k$. Demuestra que $\varphi_k^x(y) = \varphi_k(y-x)$.
- Definase $g_k(x) = \int_{-\infty}^{\infty} \varphi_k(y-x)g(y) dy$. Demuestra que $g_k$ es $C^\infty$ y que $\lim_{k \to \infty} g_k \to g$ (puntualmente). Concluye que toda función continua se puede aproximar con funciones $C^{\infty}$.
Generaliza el ejercicio anterior a $\mathbb{R}^n$.
Cubiertas y refinamientos
Recordemos que una cubierta $\mathcal{C}$ de un subconjunto $A \subset \mathbb{R}^n$ es una colección de conjuntos abiertos $\mathcal{C} \subset P(\mathbb{R}^n)$ tales que $\bigcup_{U \in \mathcal{C}} U \supset A$.
Sea $A \subset \mathbb{R}^n$ y $\mathcal{C}$ una cubierta de $A$. Una cubierta $\mathcal{C}'$ de $A$ es un refinamiento de $\mathcal{C}$, si
para todo $V \in \mathcal{C}'$ existe $U \in \mathcal{C}$ tal que $V \subset U$. En tal caso escribimos $\mathcal{C}' \subset \mathcal{C}$ y decimos también que
$\mathcal{C}'$ refina a $\mathcal{C}$.
Sea $\mathcal{C}$ una cubierta de $A$. Se dice que $\mathcal{C}$ es una cubierta localmente finita de $A$ si para todo $x \in A$ existe una vecindad abierta $x \in V_x$ tal que el conjunto
$$
\left\{ U \in \mathcal{C} | V_x \cap U \neq \emptyset \right\}
$$
es finito.
Damos un par de ejemplos:
Sea $\mathcal{C}=\left\{ \left( -n,n \right) \right\}_{n \in \mathbb{N}}$. Si $x \in \mathbb{R}$ y $N \in \mathbb{N}$ es tal que $N \geq |x|$ entonces $x \in (-N,N)$. Luego
para todo $n \geq |x|$ se tiene que $x \in (-n,n)$. Por lo tanto $\mathcal{C}$ no es una cubierta localmente finita ya que todo punto está contenido en una cantidad infinita
de elementos de $\mathcal{C}$ ¿Puedes encontrar un refinamiento localmente finito?
Sea $\mathcal{C} = \left\{ \left( n-1,n+1 \right) \right\}_{n \in \mathbb{Z}}$. A pesar de no ser una cubierta finita es localmente finita. Esto ya que si $x \in \mathbb{R}$ entonces
$B_{1/2}(x)$ intersecta a lo mas a tres elementos de $\mathcal{C}$ (demuestralo).
El ejemplo anterior es parte de una gran familia de cubiertas localmente finitas
Sea $\mathcal{C}$ una cubierta de $A$. Si para todo $U \in \mathcal{C}$ el conjunto $\left\{ V \in \mathcal{C} \mid V \cap U \neq \emptyset \right\}$ es finito entonces $\mathcal{C}$
es localmente finita.
Sea $(a,b) \subset \mathbb{R}$ un intervalo abierto y $\mathcal{C}$ una cubierta de $(a,b)$. Demuestra que $\mathcal{C}$ tiene un refinamiento localmente finito. Esto es, existe una
cubierta $\mathcal{C}'$ que refina a $\mathcal{C}$ y que es localmente finita.
Demuestra que si $A \subset \mathbb{R}$ y $\mathcal{C}$ es una cubierta de $A$ entonces $\mathcal{C}$ tiene un refinamiento localmente finito.
Particiones de la unidad
Sea $f:\mathbb{R}^n \rightarrow \mathbb{R}$. El soporte de $f$ es el conjunto
$$
sop(f) = \overline{ \left\{ x \in \mathbb{R}^n \mid f(x) \neq 0 \right\}}
$$
Sean $R\subset \mathbb{R}^n$ un rectángulo y $\varepsilon>0$. Si $g=g_R^{\varepsilon}$ es la función de la proposición demuestra que $sop(g) = R^{\varepsilon}$.
Sea $A \subset \mathbb{R}^n$ y $\mathcal{C}$ una cubierta abierta de $A$. Una partición de la unidad de $A$ subordinada a $\mathcal{C}$ es una colección de funciones $\Phi = \left\{ \varphi_{\beta}: V \rightarrow \mathbb{R} \right\}_{\beta \in B}$ tales que:
- $V$ es una vecindad abierta de $A$.
- $\varphi_{\beta}$ es $C^{\infty}$ para toda $\beta \in B$.
- Para todo $\beta \in B$ y $x \in \mathbb{R}^n$ se tiene que $0 \leq \varphi_{\beta}(x) \leq 1$.
- Para todo $\beta \in B$ el soporte $sop(\varphi_{\beta})$ es compacto y la colección de soportes $\mathcal{C}' = \left\{ sop(\varphi_{\beta}) \mid \beta \in B \right\}$ es un refinamiento localmente finito de $\mathcal{C}$.
- Para todo $x \in A$ se tiene que $$ \sum_{\beta \in B} \varphi_{\beta}(x) = 1 $$
Observemos un par de cosas. Si $f: \mathbb{R}^n \rightarrow \mathbb{R}$ y $x \notin sop(f)$ entonces $f(x) = 0$. En segundo lugar si $\Phi$ es una partición de la unidad de $A$ subordinada a $\mathcal{C}$ entonces $\mathcal{C}’=\left\{ sop(\varphi) \mid \varphi \in \Phi \right\} $ es un refinamiento localmente finito de $\mathcal{C}$. Así si $x \in A$ el conjunto $\Phi_x = \left\{ \varphi \in \Phi \mid x \in sop(\varphi) \right\}$ es finito, digamos $\Phi_x=\left\{ \varphi_1,…,\varphi_r \right\}$. Luego si $\varphi \notin \Phi_x$ entonces $x \notin sop(\varphi)$ y por lo tanto $\varphi(x) = 0$. Esto muestra que la suma es una suma finita, por lo que el inciso $5.$ tiene sentido.
Sea $A = [0,1]$ y $\mathcal{C} = \left\{ U_1,U_2 \right\}$ donde $U_1 = (-1/2,4/5)$ y $U_2 = (1/5,3/2)$. Supongamos que $\varphi_1,\varphi_2: \mathbb{R} \rightarrow \mathbb{R} $ forman
una partición de la unidad de $[0,1]$ subordinada a $\mathcal{C}$. Supongamos (sin gran perdida de generalidad) que $sop(\varphi_1) = [-1/4,3/4]$ y $sop(\varphi_2)=[1/4,5/4]$. Notemos que los soportes
forman una cubierta de $A$ y es un refinamiento (localmente finito) de $\mathcal{C}$ puesto que $sop(\varphi_1) \subset U_1$ y $sop(\varphi_2) \subset U_2$. También observemos
que los soportes son compactos. Ahora solo tenemos que encontrar las funciones $\varphi_1$ y $\varphi_2$.
Notemos que si $x \in [0,1/4]$ entonces $x \notin sop(\varphi_2)$ y luego $\varphi_2(x) = 0$, sin embargo se debe satisfacer que $\varphi_1(x) + \varphi_2(x) = 1$, por lo que
$\varphi_1(x) = 1$. Análogamente si $x \in [3/4,1]$ entonces $\varphi_2(x) = 1$. Las condiciones impuesas implican que las gráficas de las funciones se ven como en la figura.
Sea $A \subset \mathbb{R}^n$. Cualquier cubierta abierta de $A$ admite una partición de la unidad de $A$ subordinada a ella.
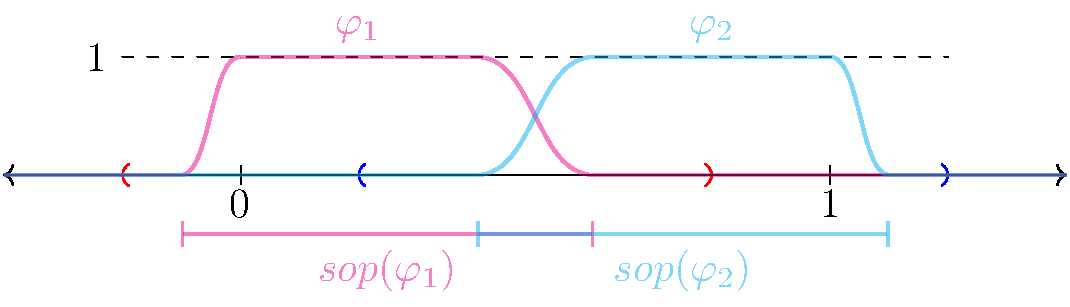
Demostraremos este teorema en etapas sucesivas.
Caso compacto
Sea $A$ un conjunto compacto y $\mathcal{C}$ una cubierta abierta de $A$.
Existe una partición de la unidad de $A$ subordinada a $\mathcal{C}$.
Sea $x \in A$. Luego existe $U \in \mathcal{C}$ tal que $x \in U$. Dado que $U$ es abierto existe $\varepsilon_x >0$ suficientemente pequeño tal que
$R_{\varepsilon_x}(x) \subset U$. Definimos $W_x = R_{\varepsilon_x}(x)$. Noten que $W_x$ es compacto y que para todo $x$ existe $U \in \mathcal{C}$ tal que $W_x \subset U$.
Por otro lado $\left\{int(W_x)\right\}_{x \in A}$ es una cubierta abierta de $A$ ya que $x \in int(W_x)$ para toda $x \in A$. Por la compacidad de $A$ podemos extraer una
subcubierta finita $\mathcal{C}'=\left\{ W_1,...,W_r \right\}$, donde $W_i = W_{x_i}$ para algunos $x_i \in X$. Notemos que $V = \bigcup_{i=1}^r int(W_x)$ es una vecindad abierta de $A$. Observen también que $W_i = W_{x_i} = R_{\varepsilon_{x_i}}(x_i)$ es compacto.
Para cada $i=1,...,r$ sean $g_i = g_{[x_i,x_i]}^{\varepsilon_{x_i}}$ (véase la proposición) y $h_i = g_i\big|_{V}$. Las funciones $h_i : V \rightarrow \mathbb{R}$ satisfacen las
siguientes condiciones:
- $h_i$ es $C^{\infty}$.
- $h_i(x) \geq 0$ para todo $x \in V$.
- Si $x \in int(W_i)$ entonces $h_i(x) \neq 0$.
- $sop(h_i) = W_i$ (véase el ejercicio ).
Notemos que en este caso la partición de la unidad es una familia finita de funciones $\Phi=\left\{ \phi_1,…,\phi_r \right\}$. De hecho
Sea $C$ un conjunto compacto y $\mathcal{C}$ una cubierta localmente finita de $C$. Si $U \cap C \neq \emptyset$ para todo $U \in \mathcal{C}$ entonces $\mathcal{C}$ es finita.
Supongamos que existe una cantidad numerable $\left\{ U_1,... \right\} \subset \mathcal{C}$ de elementos distintos de la cubierta tales que $C \cap U_i \neq \emptyset$. Sea $\left\{ x_i \right\}_{i \in \mathbb{N}}$ una sucesión de puntos con $x_i \in C \cap U_i$. Dado que $C$ es compacto la sucesión $\left\{ x_i \right\}_{i \in \mathbb{N}}$ tiene una subsucesión convergente. Podemos
suponer sin perdida de generalidad que $x_i \to x$. Por hipótesis existe $V$ vecindad abierta de $x$ tal que
$$
\Phi_x = \left\{ U \in \mathcal{C} \mid V \cap U \neq \emptyset \right\}
$$
es finito. Sin embargo dado que $x_i \to x$, existe $N \in \mathbb{N}$ tal que para todo $n \geq N$ se tiene que $x_n \in U$. Pero $x_n \in U_n$ y luego $U_n \cap U \neq \emptyset$. Esto
es una contradicción.
Caso abierto
Sea $A$ un conjunto abierto y $\mathcal{C}$ una cubierta abierta de $A$. Primero demostraremos que podemos reducir este caso a uno más general.
Para $k \in \mathbb{N}$ definimos $C_k = \left\{ x \in A | d(x,\partial A) \geq \frac{1}{k} \right\} \cap B_{k}(0) \subset A$.
Demuestra que $C_k$ es cerrado y acotado. Concluye que $C_k$ es compacto.
Demuestra que $C_{k} \subset int(C_{k+1})$ y $A = \bigcup_{k \in \mathbb{N}} C_k$.
Luego el hecho de que $\mathcal{C}$ tenga una partición de la unidad de $A$ subordinada a ella es una consecuencia de la siguiente proposición.
Sean $\left\{ C_k \right\}_{k \in \mathbb{N}}$ subconjuntos compactos de $\mathbb{R}^n$ tales que $C_k \subset int(C_{k+1})$. Si $A = \bigcup_{k \in \mathbb{N}}C_k$ y $\mathcal{C}$ es una
cubierta abierta de $A$ entonces existe una partición de la unidad de $A$ subordinada a $\mathcal{C}$.
Para cada $i \in \mathbb{N}$ definimos $B_i = C_{i} \setminus int(C_{i-1})$ (donde $C_{-1} = \emptyset$ y por lo tanto $B_0 = C_0$). Dado que $B_i$ es un conjunto cerrado menos un abierto, $B_i$
es un subconjunto cerrado de $C_i$ y por lo tanto compacto (todo subconjunto cerrado de un compacto es compacto). También sea $V_i = int(C_{i+1}) \setminus C_{i-2}$ (de nuevo $C_{-2}= \emptyset$)
y noten que $V_i$ es una vecindad abierta de $B_i$. Además definimos $\mathcal{C}_i = \left\{ U \cap V_i \mid U \in \mathcal{C} \right\}$ la cual es es una cubierta abierta de $B_i$.
Puesto que si $x \in B_i \subset A$ entonces existe $U \in \mathcal{C} $ tal que $x \in U$ y por lo tanto $x \in U \cap V_i$.
Sea $\Phi_i = \left\{ \varphi^i_j: U_i \rightarrow \mathbb{R} \right\}_{j \in J_i}$ una partición de la unidad de $B_i$ subordinada a $\mathcal{C}_i$. Por la proposición podemos
suponer que $J_i$ es un conjunto finito. Por el teorema existe una
función $C^{\infty}$, $f_i : \mathbb{R}^n \rightarrow \mathbb{R} $, tal que $f_i(x) = 1$ para todo $x \in B_i$ y $f_i(x) = 0$ para $x \in \mathbb{R}^n\setminus W_i$ (donde $W_i$ es un abierto
con $\overline{W_i} \subset U_i $). Luego la multiplicación
$f_i \cdot \varphi^i_j$ es una función $C^{\infty}$ que coincide con $\varphi^i_j$ en $B_i$ pero que puede extenderse a una función $\phi^i_j:\mathbb{R}^n \rightarrow \mathbb{R}$ definiendo
$\phi^i_j(x) = 0$ para $x \in \mathbb{R}^n \setminus U_i$. En otras palabras, si definimos
$$
\phi^i_j(x) = \begin{cases} f_i(x) \varphi^i_j(x) & x \in U_i \\ 0 & x \in \mathbb{R}^n \setminus U_i \end{cases}
$$
entonces $\phi^i_j$ es $C^{\infty}$. Observen que $sop(\phi^i_j) \subset sop(\varphi^i_j)$.
Sea $\mathcal{C}' = \left\{ sop(\varphi^i_j) \right\}_{i \in \mathbb{N}, j \in J_i}$. Demostraremos que $\mathcal{C'}$ es un refinamiento localmente finito de $\mathcal{C}$.
Sea $i\in \mathbb{N}$,
$j \in J_i$. Dado que $\Phi_i$ es una partición de la unidad para $B_i$ subordinada a $\mathcal{C}_i$ existe $U' \in \mathcal{C}_i$ tal que $sop(\varphi^i_j) \subset U'$. Por
la definición de $\mathcal{C}_i$ existe $U \in \mathcal{C}$ tal que $U' = U \cap V_i$. Luego $sop(\phi^i_j) \subset sop(\varphi^i_j) \subset U' \subset U$.
Sea $x \in A$. Existe $i \in I$ tal que $x \in B_i$. Dado que $\Phi_i$ es una partición de la unidad para $B_i$ se tiene que
$$
\sum_{j \in J_i} \varphi^i_j(x) = 1
$$
lo cual implica que existe $j \in J_i$ tal que $\varphi^i_j(x) \neq 0$. Dado que $\varphi^i_j$ y $\phi^i_j$ coinciden en $B_i$ entonces $\phi^i_j(x) \neq 0$ y por lo tanto $x \in sop(\phi^i_j)$.
Esto muestra que $\mathcal{C}'$ es un refinamiento de $\mathcal{C}$.
Para ver que $\mathcal{C}'$ es localmente finita notemos que $sop(\phi^i_j) \subset sop(\varphi^i_j) \subset U' \cap V_i \subset V_i$ y también que $V_i \cap V_j = \emptyset$ si $i\neq j-1,j,j+1$. Sea $x \in A$. Entonces $x \in B_k$ para algún $k \in \mathbb{N}$. $V_k$ es una vecindad abierta de $x$. Sin embargo $V_k$ intersecta solo a $V_{k-1},V_{k}$ y $V_{k+1}$ por lo que solo puede
intersecta a los elementos de la forma $sop(\phi^{i}_j)$ con $i = k-1,k,k+1$. Elegimos las particiones de la unidad $\Phi_i$ finitas, por lo que
$$
\left\{ \phi^i_j \mid i=k-1,k,k+1 , j\in J_i \right\}
$$
es una colección finita. Luego $\mathcal{C}'$ es localmente finita.
Finalmente sea $V = \bigcup_{i \in \mathbb{N},j \in J_i} int(sop(\phi^i_j))$. La función $\sigma(x) = \sum_{i \in \mathbb{N},j \in J_i}\phi^i_j(x)$ es una función $C^{\infty}$ y nunca es cero
en $V$ puesto que algun sumando es distinto de $0$. Sea $g^i_j : V \rightarrow \mathbb{R}$ la función definida por $g^i_j(x) = \phi^i_j(x) / \sigma(x)$. Afirmamos que $\Phi=\left\{ g^i_j \mid i \in \mathbb{N}, j \in J_i \right\}$ es una partición de la unidad de $A$ subordinada a $\mathcal{C}$. La demostración de esta afirmación depende de las observaciones previas y de un último argumento
semejante al de la demostración de la proposición anterior (cf. la proposición ). Se deja como ejercicio para el lector.
Caso general
Sea $A$ cualquier conjunto y $\mathcal{C}$ una cubierta abierta de $A$.
Sea $U = \bigcup \mathcal{C}$. Luego existe una partición de la unidad de $U$ subordinada a $\mathcal{C}$. Esta es una partición de la unidad de $A$ subordinada a $\mathcal{C}$.
Demuestra la última afirmación.
Apéndice: Diferenciabilidad de F
Sea $P$ cualquier polinómio, entonces
$$
\lim_{h \to 0^+} \frac{e^{-h^{-2}}P(1/h)}{h} = 0
$$
Recordemos que si $Q$ es cualquier polinomio entonces
$$
\lim_{x \to +\infty} \frac{Q(x)}{e^x} = 0
$$
(quien no lo recuerde utilize L'Hôpital suficientes veces). Notemos que cuando $h \to 0^+$ se tiene que $1/h \to + \infty$ y luego
$$
\lim_{h \to 0^+} \frac{e^{-h^{-2}}P(1/h)}{h} = \lim_{h \to 0^+} \frac{P(1/h)(1/h)}{e^{(1/h)^2}} = \lim_{x \to +\infty} \frac{P(x)x}{e^{x^2}}
$$
Para $x \geq 1$ se tiene que $x^2 \geq x$ y por lo tanto
$$
\left| \frac{P(x)x}{e^{x^2}} \right| \leq \left| \frac{P(x)x}{e^{x}} \right|
$$
Dado que $P(x)x = Q(x)$ es un polinomio resulta que
$$
0 \leq \lim_{x \to +\infty} \left| \frac{P(x)x}{e^{x^2}} \right| \leq \lim_{x \to +\infty} \left| \frac{Q(x)}{e^x} \right| = 0
$$
Consecuentemente
$$
\lim_{h \to 0^+} \frac{e^{-h^{-2}}P(1/h)}{h} = \lim_{x \to +\infty} \frac{P(x)x}{e^{x^2}} = 0
$$
Si $f$ es $n$ veces diferenciable entonces $f^{(n)}$ denota la $n$-ésima derivada de $f$, o equivalentemente $f^{(0)} = f$ y $f^{(n+1)} = (f^{(n)})’$.
[Demostración de la proposición 1.1]
Comenzaremos con algo un poco más general. Demostraremos que si $g$ es una función del tipo
$$
g(x) = \begin{cases} e^{-x^{-2}}P(1/x) & x> 0 \\ 0 & x \leq 0 \end{cases}
$$
con $P$ algún polinomio entonces $g$ es derivable y
$$
g'(x) = \begin{cases} e^{-x^{-2}}Q(1/x) & x>0 \\ 0 & x \leq 0 \end{cases}
$$
para otro polinomio $Q$.
Si $x < 0$ entonces $g$ es localmente constante y por lo tanto $g$ es derivable en $x$ y $g'(x) = 0$.
Si $x > 0$ entonces $g$ es derivable en $x$ ya que todas las funciones que definen a $g(x)$ (cuando $x>0$) son diferenciables para $x>0$. Además
$$
\begin{aligned}
g'(x) & = (e^{-x^{-2}}P(1/x))' = (e^{-x^{-2}})'P(1/x) + e^{-x^{-2}}(P(1/x))'\\ & = e^{-x^{-2}}\cdot (2x^{-3})P(1/x) + e^{-x^{-2}}P'(1/x)\cdot(-x^{2}) \\
& = e^{-x^{-2}}\left( 2(1/x)^3P(1/x) - (1/x)^2P'(1/x) \right) = e^{-x^{-2}}Q(1/x)
\end{aligned}
$$
donde $Q$ es el polinomio $Q(x) = 2x^3P(x) -x^2P'(x)$.
Recuerden que $g$ es continua en $x$ si y solo si las derivadas derecha $g'(x^{+})$ e izquierda $g'(x^{-})$ existen y $g'(x^{+}) = g'(x^{-})$. La derivada izquierda de $g$ en $0$ es fácil
de calcular ya que $g$ es constante para $x \leq 0$ y por lo tanto $g'(0^-) = 0$. Por otro lado, por el lema se tiene que
$$
g'(x^+) = \lim_{h \to 0^+} \frac{e^{-h^{-2}}P(1/h)}{h} = 0
$$
y luego $g$ es derivable en $0$ y $g'(0) = 0$. En resumen $g$ es derivable y
$$
g'(x) = \begin{cases} e^{-x^{-2}}Q(1/x) & x>0 \\ 0 & x \leq 0 \end{cases}
$$
Ahora notemos que $F$ es de esta forma con $P(x) = 1$. Esto implica que $F$ es derivable y que su derivada es una función del mismo tipo. Por inducción se concluye que $F$ es infinitamente
diferenciable.