Notas de vectores tangentes

Publicado el | en |

Versión en pdf.

Introducción

Las funciones diferenciables $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$ son muy útiles puesto que asumimos que tienen un comportamiento infinitesimal muy simple. A secas una función diferenciable es infinitesimalmente afín (lineal más constante). Su utilidad proviene del hecho de que podemos extrapolar información de la función simple (la diferencial de $f$) al comportamiento de la función $f$ (al menos cerca del punto). Ahora queremos usar esa estrategia en una variedad abstracta.

Ya hemos definido que una función $f: M \rightarrow N$ entre variedades es diferenciable si cada una de sus representaciones coordenadas lo es. Una representación coordenada $\tilde f$ de $f$ tiene derivada en todo punto, pero ¿qué nos está diciendo la derivada $D\tilde f$, que a fin de cuentas es una representación arbitraria de $f$, acerca de $f$?

Sea $f: U \subset \mathbb{R}^n \rightarrow \mathbb{R}^m$ una función diferenciable. La siguiente proposición brinda un método útil para calcular la diferencial de $f$ en un punto $p \in U$.

Sea $v \in \mathbb{R}^n$. Para calcular la diferencial $Df_p$ evaluada en $v$ basta con encontrar cualquier curva diferenciable $\beta: (-\varepsilon,\varepsilon) \rightarrow U$, con $\varepsilon >0$, tal que $\beta(0) = p$ y $\beta'(0) = v$. Con esta curva $$ Df_p(v) = \left( f \circ \beta \right)'(0) $$
Esto no es más que la regla de la cadena: Como $\beta$ es diferenciable en $0$ y $f$ es diferenciable en $\beta(0) = p$ entonces $f \circ \beta$ es diferenciable en $0$ y $$ (f \circ \beta)'(0) = Df_{p} (\beta'(0)) = Df_{p}(v) $$

Es importante notar que $\beta$ es cualquier curva que pase por $p$ y tenga a $v$ como vector tangente. La curva $\beta$ tiene a $v$ como dirección infinitesimal en $p$ y se transforma, bajo $f$, a una nueva curva $\alpha = f \circ \beta$, que tiene a $Df_p(v)$ como nueva dirección infinitesimal.

\todo{Imagen diferencial}

Es por eso que es posible pensar a la diferencial de $f$ en $p$ como la función que determina como se transforman las “direcciones infinitesimales” en $p$.

Vectores tangentes como curvas

Usando la observación anterior como pauta, haremos una generalización a variedades. Un vector tangente en $p \in M$ será una dirección infinitesimal, representada por una curva. Sin embargo varias curvas representan la misma dirección infinitesimal.

Sean $\alpha: I_1 \rightarrow M$ y $\beta: I_2 \rightarrow M$ dos curvas diferenciables con $I_1, I_2 \subset \mathbb{R}$ intervalos abiertos con $0 \in I_1,I_2$ tales que $\alpha(0) = \beta(0) = p \in M$. Decimos que $\alpha$ y $\beta$ representan la misma dirección infinitesimal en $p$, y lo denotamos por $\alpha \sim_p \beta$, si existe alguna carta $(U, \varphi_U)$ de $M$ cerca de $p$ tal que $$ (\varphi_U \circ \alpha)'(0) = \bar \alpha'(0) = \bar \beta'(0) = (\varphi_U \circ \beta)'(0) $$
En todo lo que sigue usaremos $\bar \delta$ para denotar a la representación coordenada de $\delta$ en una carta $(U, \varphi_U)$. Aquí $\delta$ puede ser una curva $\delta: I \rightarrow M$, en cuyo caso $\bar \delta = \varphi_U \circ \delta$, una función $\delta: M \rightarrow \mathbb{R}$, en cuyo caso $\bar \delta = \delta \circ \varphi_U^{-1}$, o simplemente un punto $\delta \in U$, en cuyo caso $\bar \delta = \varphi_U(\delta)$.

Notemos que los dominios de definición de $\alpha$ y $\beta$ no son tan relevantes, la información importante está contenida en una vecindad arbitrariamente pequeña del $0$.

\todo{imagen vector tangente}

Definimos la relación $\sim_p$ en base a la existencia de sólo una representación coordenada común para $\beta$ y $\alpha$. Sin embargo, como es usual, la relación de tener la misma dirección infinitesimal no depende de la representación coordenada elegida.

Sean $\alpha: I_1 \rightarrow M$ y $\beta: I_2 \rightarrow M$ curvas diferenciales tales que $\alpha \sim_p \beta$. Si $(V, \varphi_V)$ es cualquier carta alrededor de $p$ y $\hat \alpha = \varphi_V \circ \alpha$, $\hat \beta = \varphi_V \circ \beta$ sus representaciones coordenadas entonces $$ \hat \alpha'(0) = \hat \beta'(0) $$
Demuéstralo.
Es un tanto extraño definir la relación $\sim_p$ en base a la existencia de una carta bajo la cual sus representaciones coordenadas tienen el mismo vector tangente, cuando hemos demostrado que esto implica lo mismo para cualquier carta. Sin embargo esto es por conveniencia: de este modo para demostrar $\alpha \sim_p \beta$ basta con encontrar una carta bajo la cual $\bar \alpha'(0) = \bar \beta'(0)$, y hay veces en las cuales la elección de una carta particular simplifica mucho la demostración. Por otro lado también es útil la proposición anterior puesto que la hipótesis $\alpha \sim_p \beta$ implica que $\bar \alpha'(0) = \bar \beta'(0)$ para cualquier representación coordenada. Así que uno puede usar esta información en la carta que uno guste.
La relación $\sim_p$ es una relación de equivalencia.
Demostrar la identidad y simetría de la relación es muy sencillo, así que basta con demostrar la transitividad de la relación. Supongamos que $\alpha:I_1 \rightarrow M$, $\beta: I_2 \rightarrow M$ y $\gamma: I_3 \rightarrow M$ son tres curvas diferenciales con $\alpha(0)=\beta(0)=\gamma(0) = p$ y tales que $$ \alpha \sim_p \beta \\ \beta \sim_p \gamma $$ Esto implica que existe un par de cartas $(U, \varphi_{U})$ y $(V, \varphi_V)$ tales que si $\bar \alpha = \varphi_U \circ \alpha$, $\bar \beta = \varphi_U \circ \beta$, $\hat \beta = \varphi_V \circ \beta$ y $\hat \gamma = \varphi_V \circ \gamma$, entonces $$ \bar \alpha'(0) = \bar \beta'(0) \\ \hat \beta'(0) = \hat \gamma'(0) $$ Notemos que $\hat \alpha = \varphi_V \circ \alpha = \varphi_V \circ \varphi_U^{-1} \circ \varphi_U \alpha = \Psi_{U}^V \circ \bar \alpha$ y por lo mismo $\hat \beta = \Psi_U^V \circ \bar \beta$, donde $\Psi_U^V$ es el cambio de coordenadas de $U$ a $V$. Dado que $\Psi_U^V$ es un difeomorfismo (como función $\Psi_U^V: W \subset \mathbb{R}^n \rightarrow \mathbb{R}^n$) entonces por la regla de la cadena $$ \hat \beta'(0) = D\Psi_{U}^V(\bar \beta'(0)) = D\Psi_{U}^V(\bar \alpha'(0)) = \hat \alpha'(0) $$ pero como $\hat \gamma'(0) = \hat \beta'(0)$, entonces $\hat \gamma'(0) = \hat \alpha'(0)$, y por lo tanto $\alpha \sim_p \gamma$.

Dado que dos vectores son equivalentes si tienen la misma dirección infinitesimal (en una y por lo tanto en todas las cartas) entonces la clase de equivalencia $\left[ \alpha \right]_{\sim_p} = \left\{ \beta: I \rightarrow M \mid \beta(0) = p, \beta \sim_p \alpha \right\}$ en cierto modo representa una dirección infinitesimal, sin importar la curva que lo represente.

Un vector tangente de $M$ en $p$ es una clase de equivalencia de la relación $\sim_p$. El espacio tangente $T_pM$ es la colección de vectores tangente a $M$ en $p$: $$ \label{eq:espaciotangente} T_pM = \left\{ [\alpha]_{\sim_p} \mid \alpha: I \rightarrow M \text{ diferenciable con } \alpha(0) = p \right\} $$

Cada curva que pasa por $p$ determina un vector tangente.

Definido así, la noción de vector tangente y espacio tangente no dependen de coordenadas, sino de curvas y una noción de equivalencia de dirección. Aunque la noción de equivalencia depende de modo indirecto de cartas, hemos demostrado que realmente no depende de las coordenadas elegidas. Con esta construcción hemos ganado en generalidad, pero hemos llegado a una noción un tanto abstracta e inmanejable.

Sin embargo tiene una ventaja: con esta noción de vector tangente es fácil generalizar la definición de la diferencial de una función.

Sea $f: M \rightarrow N$ una función diferenciable y $p \in M$. La diferencial o derivada de $f$ en $p$ es la función $Df_p: T_pM \rightarrow T_{f(p)}N$ definida por $$ Df_p([\alpha]_{\sim_p}) = [f \circ \alpha]_{\sim_{f(p)}} $$ La imagen de vector tangente (clase de equivalencia de curvas) es la clase de equivalencia de la curva imagen. La diferencial de $f$ en $p$ también es denotada $T_pf, df_p, f^*_p$.

\todo{imagen diferencial}

Demuestra que la definición antes dada está bien definida, es decir no depende del representante de la clase de equivalencia. Más explícitamente: Si $\alpha: I_1 \rightarrow M$, $\beta: I_2 \rightarrow M$ son curvas diferenciables con $\alpha(0) = \beta(0)$ y $\alpha \sim_p \beta$, y $f: M \rightarrow N$ es una función diferenciable entre variedades, entonces $f \circ \alpha \sim_{f(p)} f \circ \beta$.

La definición anterior es una calca de la proposición. Sin embargo, en la versión clásica de la diferencial podíamos afirmar que dicha función además era lineal.

Para transferir esa proposición al caso general habría que empezar con brindarle al espacio tangente $T_pM$ una estructura de espacio vectorial. Aunque esto no es difícil, sí es un poco engorroso.

Sea $p \in M$ y $(U, \varphi_U)$ una carta alrededor de $p$. Dado que estamos trabajando en un único punto, podemos dispensar de la notación saturada de $\left[ \alpha \right]_{\sim_p}$ para reemplazarla temporalmente por $[\alpha]$, esto es, por el momento (o mientras no haya confusión con la relación y el punto en cuestión) $[\alpha] = \left[ \alpha \right]_{\sim_p}$. Definimos una estructura de espacio vectorial en $T_pM$ de la siguiente manera:
  1. Si $\left[ \alpha \right], \left[ \beta \right] \in T_pM$ entonces $$ \left[ \alpha \right] + \left[ \beta \right] = \left[ \varphi_{U}^{-1}\left( \bar \alpha + \bar \beta - \bar p \right) \right] $$
  2. Si $c \in \mathbb{R}$ y $\left[ \alpha \right] \in T_pM$ entonces $$ c \left[ \alpha \right] = \left[ \varphi_{U}^{-1}\left( c \bar \alpha - (c-1) \bar p \right) \right] $$
$\varphi_U$ brinda un modo de representar curvas $\alpha$ y $\beta$ con coordenadas, a saber $\bar \alpha = \varphi_U \circ \alpha$ y $\bar \beta = \varphi_U \circ \beta$. Estas son curvas que en $0$ pasan por $\bar \alpha(0) = \bar \beta(0) = \varphi_U(\beta(0)) = \varphi_U(p) = \bar p$. Cada una tiene un vector tangente en $0$ distinto, digamos $v= \bar \alpha'(0)$ y $w = \bar \beta'(0)$. Por tanto la suma de dichas curvas $\bar \alpha + \bar \beta$ es una curva que tiene como vector tangente $(\bar \alpha + \bar \beta)'(0) = v+w$. Sin embargo en $0$ pasa por $(\bar \alpha + \bar \beta)(0) = \bar \alpha(0) + \bar \beta(0) = 2\bar p$, luego la curva $$ \bar \alpha + \bar \beta - \bar p $$ Es una curva que pasa por $\bar p$ en $0$ y tiene a $v + w$ como vector tangente. Por tanto, esta curva es buen representante de la suma de las direcciones de $\alpha$ y $\beta$, por lo que basta transportarla de regreso a $M$ con la carta $\varphi_U^{-1}$ para obtener la curva que debería de representar la suma de direcciones. Esto es lo que hemos hecho: $$ \left[ \alpha \right] + \left[ \beta \right] = \left[ \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p \right) \right] $$ Una linea de pensamiento similar justifica la definición de $c[\alpha]$. Hay que ser cuidadosos con algunos detalles de los dominios, puesto que la suma sólo estaría definida en la intersección de los dominios, y a su vez las curvas $\bar \alpha, \bar \beta$ sólo están definidas cuando caen en el pedazo de espacio representado con coordenadas, i.e. $U$. Estas consideraciones se dejan para el ejercicio del lector.

\todo{imagen suma de curvas}

En el apéndice demostramos que las operaciones de suma y producto por escalar están bien definidas y que con ellas $T_pM$ es un espacio vectorial.

Ya que hemos definido la estructura de espacio vectorial podemos demostrar que la diferencial es una transformación lineal.

Sea $f: M \rightarrow N$ una función diferenciable entre variedades y $p \in M$. La diferencial $Df_p: T_pM \rightarrow T_{f(p)}N$ es una transformación lineal.
Usaremos la siguiente notación: $[\alpha]_{\sim_p} = [\alpha]_p$ y $\left[ \beta \right]_{\sim_{f(p)}} = \left[ \beta \right]_{f(p)}$. Sean $\left[ \alpha \right]_p, \left[ \beta \right]_p \in T_pM$ dos vectores. Queremos demostrar que
$$ Df_p(\left[ \alpha \right]_p + \left[ \beta \right]_p) = Df_{p}\left(\left[ \alpha \right]_p\right) + Df_p\left( \left[ \beta \right]_p \right) $$
Sean $(U, \varphi_U)$ y $(V, \varphi_V)$ cartas de $M$ y $N$ alrededor de $p$ y $f(p)$ respectivamente. Usaremos $\bar \delta$ para denotar la representación de $\delta$ con $\varphi_U$, i.e. $\bar \delta = \varphi_U \circ \delta$, y $\hat \delta$ para denotar la representación de $\delta$ con $\varphi_V$, i.e. $\hat \delta = \varphi_V \circ \delta$. Luego el vector $\left[ \alpha \right]_p + \left[ \beta \right]_p$ está representado por $$ [\gamma]_p = \left[ \alpha \right]_p + \left[ \beta \right]_p = \left[ \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p \right) \right]_p $$ y por lo tanto $$ \begin{aligned} Df_p([\alpha]_p + \left[ \beta \right]_p) & = Df_p\left( \left[ \gamma \right]_p \right) \\ & =\left[ f \circ \gamma \right]_{f(p)} \\ & = \left[ f \circ \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p \right) \right]_{f(p)} = \left[ \nu_1 \right]_{f(p)} \end{aligned} $$ Por otro lado $Df_p(\left[ \alpha \right]_p) = \left[ f \circ \alpha \right]_{f(p)}$ y $Df_p\left( \left[ \beta \right]_p \right) = \left[ f \circ \beta \right]_{f(p)}$, por lo que $$ \begin{aligned} Df_p(\left[ \alpha \right]_p) + Df_p\left( \left[ \beta \right]_p \right) & = \left[ f \circ \alpha \right]_{f(p)} + \left[ f \circ \beta \right]_{f(p)} \\ & = \left[ \varphi_V^{-1}\left( \varphi_V \circ f \circ \alpha + \varphi_V \circ f \circ \beta - \varphi_V(f(p)) \right) \right]_{f(p)} \\ & = \left[ \nu_2 \right]_{f(p)} \end{aligned} $$ Así, demostrar la ecuación es equivalente a demostrar que $\nu_1 \sim_{f(p)} \nu_2$. Para esto usamos la carta $(V, \varphi_V)$ para representar con coordenadas las curvas $\nu_1$ y $\nu_2$. Noten que $$ \begin{aligned} \hat \nu_1& = \varphi_V \circ \nu_1 = \varphi_V \circ f \circ \varphi_U^{-1} \left( \bar \alpha + \bar \beta - \varphi_U(p) \right) \\ & = \tilde f \circ \left( \bar \alpha + \bar \beta - \varphi_U(p) \right) \end{aligned} $$ y además $$ \begin{aligned} \hat \nu_2 & = \varphi_V \circ f \circ \alpha + \varphi_V \circ f \circ \beta - \varphi_V(f(p)) \\ & = \varphi_V \circ f \circ \varphi_U^{-1} \circ \varphi_U \alpha + \varphi_V \circ f \circ \varphi_U^{-1} \circ \varphi_U \circ \beta - \varphi_V(f(p)) \\ & = \tilde f \circ \bar \alpha + \tilde f \circ \bar \beta - \varphi_V(f(p)) \end{aligned} $$ Por la regla de la cadena $$ \hat \nu_1'(0) = D\tilde f_{\varphi_U(p)}\left( \bar \alpha'(0) + \bar \beta'(0) \right) = D \tilde f_{\varphi_U(p)}(\bar \alpha'(0)) + D \tilde f_{\varphi_U(p)}(\bar \beta'(0)) = \hat \nu_2'(0) $$ En conclusión $\hat \nu_1'(0) = \hat \nu_2'(0)$, $\nu_1 \sim_{f(p)} \nu_2$ y por lo tanto $Df_{p}([\alpha] + \left[ \beta \right]) = Df_p\left( \left[ \alpha \right] \right) + Df_p(\left[ \beta \right])$.
Demuestra que $Df_p(c\left[ \alpha \right]_p) = c Df_p(\left[ \alpha \right])$.

Vectores tangentes como derivaciones

Como hemos visto, manejar a los vectores tangentes como clases de equivalencia de curvas puede llegar a ser bastante tedioso. Aunque la idea de una clase de equivalencia como representante de una dirección infinitesimal es relativamente directa, ahora hemos de dejar de lado la idea geométrica de un vector tangente como una dirección infinitesimal dada por una curva para adoptar otra visión que frecuentemente facilita el trabajo.

Comencemos en $\mathbb{R}^n$. En $\mathbb{R}^n$ toda dirección infinitesimal $\left[ \alpha \right]$ puede ser representada fielmente por su vector tangente $\alpha’(0)$. Y todo vector $v \in \mathbb{R}^n$ representa una dirección infinitesimal, puesto que define una curva $\alpha_v^p(t) = p + tv$ que lo tiene como vector tangente.

Formaliza el párrafo anterior demostrando que $\psi: T_p \mathbb{R}^n \rightarrow \mathbb{R}^n$ dado por $\left[ \alpha \right] \mapsto \alpha'(0)$ es un isomorfismo.

Así que en $\mathbb{R}^n$ podemos identificar los vectores tangentes con vectores en $\mathbb{R}^n$. Una modo de representar direcciones infinitesimales lo proveen las curvas, sin embargo ahora las usaremos las “derivaciones” para representarlas.

Sea $M$ una variedad. El álgebra de funciones diferenciables es $$ C^{\infty}(M) = \left\{ f: M \rightarrow \mathbb{R} \mid f \text{ es de tipo } C^{\infty} \right\} $$ Notemos que en $C^{\infty}(M)$ se pueden sumar y multiplicar funciones puntualmente. En particular las funciones de $C^{\infty}(M)$ se pueden multiplicar por constantes $c \in \mathbb{R}$, haciéndolo un $\mathbb{R}$-espacio vectorial.

Para cada $v \in \mathbb{R}^n$ (que estamos pensando como una dirección infinitesimal en $p \in \mathbb{R}^n$) podemos definir un operador

como

Esto es $D_v^p$ es la derivada direccional en $p$, en la dirección de $v$.

El operador $D_v^p$ satisface
  1. $D_v^p$ es lineal.
  2. $D_v^p(fg) = D_v^p(f) g(p) + f(p) D_v^p(g)$
Sean $f,g \in C^{\infty}(\mathbb{R}^n)$ y $c \in \mathbb{R}$. Sea $\alpha: \mathbb{R} \rightarrow \mathbb{R}^n$ la curva dada por $\alpha(t) = p + tv$. Luego para toda $h \in C^{\infty}(M)$ $$ D_v^p(h) = \lim_{t \to 0} \frac{h(p+tv)-h(p)}{t} = \left( h \circ \alpha \right)'(0) $$ Por lo tanto $$ \begin{aligned} D_v^p(f+c g) & = \left((f + cg)\circ \alpha\right)'(0) \\ & = \left( f \circ \alpha \right)'(0) + c \left( g \circ \alpha \right)'(0) \\ & = D_v^p (f) + c D_v^p(g) \end{aligned} $$ Y también $$ \begin{aligned} D_v^p(fg) & = \left( (fg) \circ \alpha \right)'(0) \\ & = ((f \circ \alpha)(g \circ \alpha))'(0) \\ & = \left( f \circ \alpha \right)'(0) \left( g \circ \alpha \right)(0) + (f \circ \alpha)(0)(g \circ \alpha)'(0) \\ & = D_v^p(f) g(p) + f(p) D^p_v(g) \end{aligned} $$

Resulta que los operadores derivadas direccionales son buenos representantes de vectores en el siguiente sentido

Si $v \neq w$ entonces $D_v^p \neq D_v^p$.
Decir que dos operadores $T,S : V \rightarrow \mathbb{R}$ son diferentes (o iguales) es decir que existe $v \in V$ tal que $T(v) \neq S(v)$ (para todo $v \in V$ se tiene que $T(v) =S(v)$). Luego para demostrar que $D_v^p \neq D_w^p$ hay que encontrar alguna función $f \in C^{\infty}(\mathbb{R}^n)$ tal que $D_v^p(f) \neq D_w^p(f)$. Los operadores de derivada direccional $D^p_v$ miden la tasa de cambio infinitesimal de la función $f$ en la dirección de $v$, por lo que basta con encontrar una función que varíe de modo distinto en la dirección $v$ que en la dirección $w$. Existen infinidad de funciones con estas propiedades, pero daremos una que es práctica por su simplicidad. Sea $f(x) = x \cdot v - x \cdot w$. Es claro que $f$ es diferenciable y que además $$ \begin{aligned} D_z^p(f)& = \lim_{h \to 0} \frac{f(p+hz) - f(p)}{h} \\ & = \lim_{h\to 0}\frac{(p+hz)\cdot v - (p+hz)\cdot w - p\cdot v + p\cdot w}{h} \\ & = z\cdot (v - w) \end{aligned} $$ Luego $D_v^p(f) = v \cdot (v - w) \neq w \cdot (v - w ) = D_w^p(f)$ puesto que de lo contrario $(v - w) \cdot (v-w) = 0$ lo cual implica $v = w$.

Ahora que hemos visto que las derivadas direccionales sirven para representar vectores, y que además satisfacen ciertas propiedades fácilmente generalizables, no es descabellado pensar que una abstracción de este concepto podría servir para capturar la noción de espacio tangente.

Sea $M$ una variedad diferenciable y $p \in M$. Una derivación en $p$ es una transformación lineal $$ D: C^{\infty}(M) \rightarrow \mathbb{R} $$ tal que $$ D(fg) = D(f)g(p) + f(p) D(g) $$ El conjunto de derivaciones en $p$ es denotado por $$ \mathscr{D}_p = \left\{ D: C^{\infty}(M) \rightarrow \mathbb{R} \mid D \text{ es derivación} \right\} $$

Si $D$ es una derivación y $f$ es una función constante, digamos $f(p) = c$ para toda $p$, entonces $D(f) = 0$. Para ver esto podemos escribir a $f$ como $f = c \boldsymbol{1}$ donde $\boldsymbol{1}$ es la función con $\boldsymbol{1}(p) = 1$ para todo $p \in M$. Luego $D(f) = cD(\boldsymbol{1}) = c D(\boldsymbol{1}\cdot \boldsymbol{1}) = c\left( D(\boldsymbol{1}) 1 + 1 D(\boldsymbol{1}) \right) = 2c D(\boldsymbol{1})$. De aquí se sigue que $D(f) = 0$.

Las derivaciones “son” como operadores de derivada direccional, cada derivación representa derivar en una dirección. Así otro modo de definir espacio tangente en $p$ sería a través de las derivaciones $\mathscr{D}_p = T_pM$. Pero habría que justificar dicha afirmación, puesto que ya tenemos otra noción de vector tangente.

En primero lugar observemos que

El conjunto de derivaciones en $p$ es un espacio vectorial.
Para esto basta con definir la suma y la multiplicación por escalares. Notemos que si $D,S \in \mathscr{D}_p$ son un par de derivaciones y $c \in \mathbb{R}$ entonces se puede definir derivaciones $$\label{eq:sumaderivaciones} (D+S)(f) = D(f) + S(f) \\ (cD)(f) = c D(f) $$ Verificar que con estas operaciones $\mathscr{D}_p$ es un espacio vectorial es sencillo.

Como en el caso de curvas diferenciales como vectores tangentes, es relativamente fácil definir la derivada de una función en términos de derivaciones.

Sea $f: M \rightarrow N$ una función diferenciable y $p \in M$. La diferencial de la función $Df_p^*: \mathscr{D}_{p} \rightarrow \mathscr{D}_{f(p)}$ está definida de la siguiente manera: Si $D \in \mathscr{D}_p$ es una derivación, entonces $Df^*_p(D)$ es la derivación en $f(p)$ tal que para todo $g \in C^{\infty}(N)$ se tiene que $$ (Df_p^*(D))(g) = D(g \circ f) $$
El caso de $\mathbb{R}^n$: Sea $f: U \subset \mathbb{R}^n \rightarrow \mathbb{R}^m$ una función diferenciable, $p \in U$ y $v \in \mathbb{R}^n$. La función $f$ transforma a la dirección $v$ en el vector $w=Df_p(v)$. A cada vector se le asocia su operador de derivada direccional correspondiente, $D_v^p$ y $D^{f(p)}_w$. Notemos que si $h: \mathbb{R}^m \rightarrow \mathbb{R}$ entonces $$ \begin{aligned} D^{f(p)}_w(h) & = Dh_{f(p)}(w) \\ & = Dh_{f(p)}(Df_p(v))\\ & = D(h \circ f)_p(v) \\ & = D_v^p(f \circ h) \\ & = Df^*_p(D_v^p)(h) \end{aligned} $$ Luego $D^{f(p)}_w = D^{*}_p(D_v^p)$. Esto es, la diferencial $Df^*_p$ es compatible con la diferencial clásica $Df$.

Regresamos a la demostración de la afirmación de que la noción de vector tangente con curvas es compatible y equivalente a la dada por derivaciones.

Sea $M$ una variedad diferenciable y $p \in M$. La función $\Psi_p: T_pM \rightarrow \mathscr{D}_p$ dada por
$$ \Psi_p([\alpha])(f) = (f \circ \alpha)'(0) $$
es un isomorfismo lineal.
Notemos que $\Psi_p$ toma una clase de curvas $\left[ \alpha \right]$ y produce una derivación $\Psi_p(\left[ \alpha \right])$. Dicha derivación actúa sobre las funciones según la fórmula. Hay que verificar un par de cosas antes de poder continuar con la demostración de que es un isomorfismo lineal. En primera: que la función $\Psi_p$ está bien definida. Esto es, no depende del representante de clase tomado. Sean $\alpha$ y $\beta$ curvas diferenciables tales que $\alpha \sim_p \beta$ y sea $(U, \varphi_U)$ cualquier carta alrededor de $p$. Por hipótesis $\bar \alpha'(0) = \bar \beta'(0)$ (donde $\bar \delta$ denota la representación en coordenadas dada por la carta) y por lo tanto $$ \begin{aligned} (f \circ \alpha)'(0) & = (f \circ \varphi_U^{-1} \circ \varphi_U \circ \alpha)'(0) \\ & = (\bar f \circ \bar \alpha)'(0) \\ &= D\bar f_{\bar \alpha(0)} (\bar \alpha'(0)) \\ & = D \bar f_{\bar \beta(0)}(\beta'(0)) \\ & = (f \circ \beta)'(0) \end{aligned} $$ Esto prueba que la función $\Psi_p$ está bien definida. En segundo lugar tenemos que demostrar que en efecto $\Psi_p(\left[ \alpha \right])$ es una derivación. Sin embargo esto es fácil de mostrar y se deja al lector a que lo piense. Notemos que acabamos de demostrar también que se puede calcular $\Psi_p(\left[ \alpha \right])(h)$ en cualquier representación coordenada local como
$$ \begin{aligned} \Psi_p(\left[ \alpha \right])(h) & \left( \bar h \circ \bar \alpha \right)'(0) \\ &= D \bar h_{\bar p}( \bar \alpha'(0)) \\ & = \nabla \bar h(\bar p) \cdot \bar \alpha'(0)\\ & = \frac{\partial \bar h}{\partial x_i}(\bar p) \bar \alpha'(0)^i \end{aligned} $$
donde $\bar p$ es la representación coordenada de $p$. Sean $\left[ \alpha \right], \left[ \beta \right] \in T_pM$ y $c \in \mathbb{R}$. Recordemos que podemos representar localmente a $[\alpha] + c\left[ \beta \right] = \left[ \delta \right]$ como $$ \bar \delta = \bar \alpha + c \bar \beta - c \bar p $$ Luego, por la ecuacion, para toda $h \in C^{\infty}(M)$ $$ \begin{aligned} \Psi_p(\left[ \alpha \right] + c\left[ \beta \right])(h) & = D \bar h_{\bar p} \left( \bar \delta'(0) \right) \\ & = D\bar h_{\bar p}\left( \bar \alpha'(0) + c\bar \beta'(0) \right) \\ & = D\bar h_{\bar p}\left( \bar \alpha'(0)\right) + cD \bar h_{\bar p}(\bar \beta'(0)) \\ & = \Psi_p\left( \left[ \alpha \right] \right)(h) + c \Psi\left( \left[ \beta \right] \right)(h) \end{aligned} $$ Por lo que $\Psi_p(\left[ \alpha \right] + c \left[ \beta \right]) = \Psi_p(\left[ \alpha \right]) + c \Psi_p(\left[ \beta \right])$, es decir $\Psi_p$ es lineal. Ahora queremos demostrar que $\Psi_p$ es inyectiva, lo cual equivale a demostrar que $Nuc(\Psi_p) = \left\{ 0 \right\}$. Sea $[\alpha] \neq 0$ un vector tangente. Ver que $\Psi_p(\left[ \alpha \right]) \neq 0$ es exhibir una función $h \in C^{\infty}(M)$ tal que $\Psi_p(\left[ \alpha \right])(h) = D \bar h_{\bar p}(\bar \alpha'(0)) \neq 0$, en alguna representación coordenada. Esto es encontrar alguna función que no se mantenga constante en la dirección determinada por $\alpha$. Puesto que $\left[ \alpha \right] \neq 0$ para cualquier representación coordenada $\bar \alpha'(0) \neq 0$. Aunque esto suena relativamente sencillo de demostrar, construir dicha función requiere un poco más de trabajo y lo dejamos para un apéndice. Demostraremos ahora la suprayectividad. Sea $D \in \mathscr{D}_p$ cualquier derivación en $p$. Para demostrar que proviene de una curva usaremos una representación local. Tomemos $(U, \varphi_U)$ una carta alrededor de $p$. Luego para toda $h \in C^{\infty}(M)$ y todo vector tangente $\left[ \alpha \right] \in T_pM$ sabemos que $$ \Psi_p(\left[ \alpha \right])(h) = \left( \bar h \circ \bar \alpha \right)'(0) $$ Digamos que existen funciones $h_i$ (véase apéndice) en $M$ tales que $\bar h_i(y) = y_i$ (la coordenada i-ésima de $y$) cerca de $\bar p$. Entonces en este caso $$ \Psi_p(\left[ \alpha \right])(h_i) = ( \bar h_i \circ \bar \alpha ) '(0) = \bar \alpha_i'(0) $$ es decir al derivar la función $h_i$ con la derivación $\Psi_p(\left[ \alpha \right])$ obtenemos la $i$-ésima coordenada del vector $\bar \alpha'(0)$. Con esta información se puede reconstruir el vector $\bar \alpha'(0)$. Luego, suena razonable pensar que si $v = (D(h_1),\cdots,D(h_n))$ entonces $v$ es el vector tangente de la curva que buscamos, o al menos de su representación coordenada. Es decir, nos gustaría demostrar que si $\left[ \alpha \right]$ es un vector tangente con $\bar \alpha_i'(0) = Dh_i$ entonces $\Psi_p(\left[ \alpha \right]) = D$. Esto también requiere más de lo esperado. Demostraremos una proposición similar pero algo simplificada puesto que sólo trabajaremos en $\mathbb{R}^n$. Haremos una prueba de que toda derivación de $p \in \mathbb{R}^n$ proviene de una curva. Sea $D \in \mathscr{D}_p$ con $p \in \mathbb{R}^n$. Como ya mencionamos previamente, se espera que, si $x_i : \mathbb{R}^n \rightarrow \mathbb{R}$ es la función que da la coordenada i-ésima entonces $v = (Dx_1, \cdots, Dx_n)$ es el vector para el cual $D = D_v^p$. Es decir que la derivación abstracta no es más que la derivada direccional en la dirección de $v$. Sabemos que que derivan del mismo modo las funciones $x_i$ puesto que $D_v^p(x_i) = v_i = Dx_i$. Pero el caso general requiere un lema
[Lema de Hadamard] Sea $h: \mathbb{R} \rightarrow \mathbb{R}$ una función diferenciable y $x \in \mathbb{R}^n$. Entonces existen funciones $g_i: \mathbb{R}^n \rightarrow \mathbb{R}$ diferenciables tales que $$ h(y) = h(x) + \sum_{i=1}^n(y_i-x_i)g_i(y) $$
Sea $y \in \mathbb{R}^n$ y consideremos la curva $\alpha(t) = x + t(y-x)$. Noten que $\alpha(0) = x$ y $\alpha(1) = y$, y que $\alpha$ es diferenciable. La composición $k(t) = h(\alpha(t))$ es diferenciable y por el segundo teorema fundamental del cálculo $$ \int_0^1 k'(t) dt = h(\alpha(1)) - h(\alpha(0)) = h(y) - h(x) $$ Por otro lado $$ \begin{aligned} k'(t) & = Dh_{\alpha(t)}\left( \alpha'(t) \right) \\ & = \nabla h(\alpha(t)) \cdot \alpha'(t) \\ & = \nabla h(x + t(y-x)) \cdot (y-x) \\ & = \sum_{i=1}^n \frac{\partial h}{\partial x_i}(x +t (y-x))(y_i-x_i) \end{aligned} $$ Por lo que $$ \begin{aligned} h(y) - h(x) & = \int_0^1 \sum_{i=1}^n \frac{\partial h}{\partial x_i}(x + t(y-x))(y_i-x_i) dt \\ & = \sum_{i=1} (y_i-x_i) \int_0^1 \frac{\partial h}{\partial x_i}(x + t(y-x)) dt \end{aligned} $$ Luego si $g_i(y) = \int_0^1 \frac{\partial h}{\partial x_i}(x + t(y-x)) dt$ entonces $$ h(y) = h(x) + \sum_{i=1}^n (y_i-x_i)g_i(y) $$ Por último, notemos que $g_i(x) = \int_0^1 \frac{\partial h}{\partial x_i}(x) dt = \frac{\partial h}{\partial x_i}(x)$.
Sea $h \in C^{\infty}(\mathbb{R}^n)$ cualquier función diferenciable. Por el lema de Hadamard existen $g_i$ tales que $h(x) = h(p) + \sum_{i=1}^n (x_i-p_i)g_i(x)$. Luego $$ \begin{aligned} Dh & = Dh(p) + \sum_{i=1}^n D\left( (x_i-p_i) g_i(x) \right) \\ & = \sum_{i=1}^n \left[ D(x_i-p_i) g_i(p) + (p_i-p_i)D(g_i) \right] \\ & = \sum_{i=1}^n D(x_i) \frac{\partial h}{\partial x_i}(p) \\ & = \sum_{i=1}^n v_i \frac{\partial h}{\partial x_i}(p) \\ & = D^p_v(h) \end{aligned} $$ y por lo tanto $D = D^p_v$. Esto demuestra, en el caso $M = \mathbb{R}^n$, que $\Psi_p$ es suprayectiva.
Termina la demostración de que $\Psi_p$ es isomorfismo en el caso general.

Con esto hemos terminado de demostrar que podemos pensar a cualquier vector tangente de dos modos, como una derivación o como una familia de curvas que apuntan en la misma dirección infinitesimal. El uso de una u otra visión es cuestión de conveniencia.

Definimos dos versiones diferentes de la diferencial de una función $f: M \rightarrow N$: una que depende de la noción de curvas y otra de la noción de derivaciones. La siguiente proposición afirma que las dos nociones coinciden cuando se usa el isomorfismo $\Psi_p$ para traducir una versión de vector tangente a la otra.

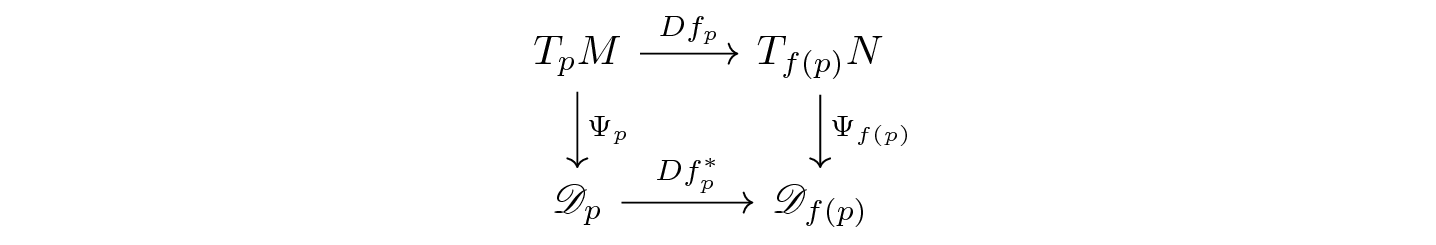Sea $f: M \rightarrow N$ una función diferenciable y $p \in M$. Sean $\Psi_p: T_pM \rightarrow \mathscr{D}_p$ y $\Psi_{f(p)}: T_{f(p)}N \rightarrow \mathscr{D}_{f(p)}$ los isomorfismos de la proposición. Para todo $v \in T_pN$ se cumple que $$ \Psi_{f(p)}(Df_p(v)) = Df^*_p(\Psi_p(v)) $$ O bien el diagrama conmuta.
Sea $\left[ \alpha \right] \in T_pM$ un vector tangente. Queremos demostrar que $\Psi_{f(p)}(Df_p(\left[ \alpha \right])) = Df^*_p(\Psi_p(\left[ \alpha \right]))$ como derivaciones (esta igualdad es en el espacio de derivaciones en $f(p)$). Luego hemos de demostrar que para toda $h \in C^{\infty}(M)$ se tiene que $$ \Psi_{f(p)}\left( Df_p\left( \left[ \alpha \right] \right) \right)(h) = Df^*_p\left( \Psi_p\left( \left[ \alpha \right] \right) \right)(h) $$ Esto no es más que desenvolver las definiciones. Por una parte $$ \begin{aligned} \Psi_{f(p)}\left( Df_{p}\left( \left[ \alpha \right] \right) \right)(h) & = \Psi_{f(p)}\left( \left[ f \circ \alpha \right] \right)\left( h \right) \\ & = (h \circ f \circ \alpha)'(0) \end{aligned} $$ Por otro lado $$ \begin{aligned} Df^*_p\left( \Psi_p\left( \left[ \alpha \right] \right) \right)(h) & = \Psi_p\left( \left[ \alpha \right] \right)(h \circ f) \\ & = \left( h \circ f \circ \alpha \right)'(0) \end{aligned} $$ Los dos términos coinciden.

De ahora en adelante todo vector $v \in T_pM$ será, al mismo tiempo, una clase de equivalencia de curvas que pasan por $p$ y tienen la misma dirección infinitesimal y una derivación en $p$. Así si $v= \left[ \alpha \right]$ y $f \in C^{\infty}(M)$ entonces

Estamos escondiendo a $\Psi_p$ para aliviar la notación.

Representaciones coordenadas

Ahora que definimos correctamente la noción de un vector tangente en una variedad abstracta daremos una descripción de los vectores tangentes en términos de coordenadas. Así que fijemos una carta $(U, \varphi_U)$ con la cual poner coordenadas en los puntos de $U$.

Tomemos $p \in M$ y sea, como es usual, $\bar p = \varphi_U(p)$. Cada curva $\alpha: I \rightarrow M$ que pasa por $p$, es decir $\alpha(0) = p$, tiene una representación coordenada $\bar \alpha = \varphi_U \circ \alpha$ que pasa por $\bar p$ en $0$. Esta curva tiene un vector tangente en $\bar p$, el cual representa la dirección infinitesimal de $\bar \alpha$ en $\bar p$. Esta receta define un mapeo

definido por

que a cada vector tangente le da su representación coordenada.

La representación coordenada del vector $\left[ \alpha \right]_p \in T_pM$ en la carta $(U, \varphi_U)$ es $\Upsilon_p(\left[ \alpha \right]) = \bar \alpha'(0) = (\varphi_U \circ \alpha)'(0)$.
La transformación $\Upsilon_p$ es un isomorfismo lineal.
Demostraremos primero que $\Upsilon_p$ es lineal. Sean $\left[ \alpha \right], \left[ \beta \right] \in T_pM$ y $c \in \mathbb{R}$. Entonces la representación coordenada de $\left[ \alpha \right] + c\left[ \beta \right] = \left[ \gamma \right]$ es $$ \bar \gamma = \bar \alpha + c \bar \beta - c \bar p $$ Por lo que $$ \Upsilon_p(\left[ \gamma \right]) = \bar \gamma'(0) = \bar \alpha'(0) + c\bar \beta'(0) = \Upsilon_p(\left[ \alpha \right]) + c\Upsilon_p\left( \left[ \beta \right] \right) $$ es decir $$ \Upsilon_p\left( \left[ \alpha \right] + c \left[ \beta \right] \right) = \Upsilon_p\left( \left[ \alpha \right] \right) + c \Upsilon_p(\left[ \beta \right]) $$ y luego $\Upsilon_p$ es lineal. Si $\left[ \alpha \right]$ y $\left[ \beta \right]$ son tales que $\Upsilon_p(\left[ \alpha \right]) = \Upsilon_p(\left[ \beta \right])$ entonces $\bar \alpha'(0) = \bar \beta'(0)$, lo cual implica $\alpha \sim_p \beta$ y $\left[ \alpha \right] = \left[ \beta \right]$. Sea $v \in \mathbb{R}^n$ y consideremos la curva diferenciable $\bar \alpha_v(t) = \bar p + tv$. Esta curva podría pensarse como la representación coordenada de la curva $\alpha_v = \varphi_U^{-1} \circ \bar \alpha(t)$. Dicha curva representa un vector tangente $\left[ \alpha_v \right] \in T_pM$ para el cual $\Upsilon_p(\left[ \alpha_v \right]) = \bar \alpha_v'(0) = v$. En conclusión $\Upsilon_p$ es un isomorfismo lineal.

La demostración anterior también nos da el isomorfismo inverso:

En particular, para cada punto de $U$, la representación coordenada induce una base de $T_pM$, llamada la base canónica inducida por la carta $(U,\varphi_U)$, dada por $\left\{ \Upsilon_p^{-1}(e_i)\right\} $, donde $\left\{ e_1,\cdots,e_n \right\}$ es la base canónica de $\mathbb{R}^n$. A estos vectores se les denota por

La base canónica de $T_pM$ inducida por la carta $(U,\varphi_U)$ es $\left\{ (\partial x_i)_p \right\}_{i=1}^n$ donde $$ (\partial x_i)_p = \left[ \varphi_U^{-1}(\bar p + te_i) \right] $$ donde $\bar p = \varphi_U(p)$.

\todo{imagen vectores canónicos}

Si el punto $p \in M$ es claro del contexto, entonces escribiremos simplemente $\partial x_i$. Es común encontrarlos en la literatura como $\partial x_i = \partial_i = \frac{\partial}{\partial x_i}$.

Todo vector $\left[ \alpha \right] \in T_pM$ puede expresarse en términos de esta base:

Aplicando $\Upsilon_p$ a ambos lados de la ecuación se obtiene

por lo que $(a^1,\cdots,a^n) = \bar \alpha’(0)$. Entonces

$$ \left[ \alpha \right]_p = \bar \alpha'(0)^i \partial x_i $$

En términos de derivaciones podemos decir lo siguiente:

El vector tangente $\partial x_i$ en $p$ actúa en las funciones $C^{\infty}(M)$ de la siguiente manera: Para todo $f \in C^{\infty}(M)$ $$ \partial x_i(f) = \frac{\partial \bar f}{\partial x_i}(\bar p) $$ donde $\bar f = f \circ \varphi_U^{-1}$ es la representación coordenada de $f$ dada por la carta $(U, \varphi_U)$.

De aquí que al vector $\partial x_i$ también se le llame $\frac{\partial}{\partial x_i}$.

Recordemos (véase la proposición) que para ver a vector tangente descrito como una clase de curvas $v = \left[ \alpha \right] \in T_pM$ como una derivación se hace lo siguiente, si $f \in C^{\infty}(M)$ $$ v(f) = \left( \alpha \circ f \right)'(0) $$ o bien como en la ecuación: $$ v(f) = \left( \bar f \circ \bar \alpha \right)'(0) $$ Sea $f \in C^{\infty}(M)$. Dado que la representación coordenada de $\partial x_i$ es $\bar p + te_i$ tenemos que $$ \partial x_i(f) = \left( \bar f(\bar p +t e_i) \right)'(0) = \frac{\partial \bar f}{\partial x_i}(\bar p) $$

Así si $v$ es cualquier vector $T_pM$ entonces podemos escribir

y luego

Ahora estudiaremos la representación coordenada de la diferencial de una función. Sea $f:M \rightarrow N$ una función diferenciable, $p \in M$, $(U, \varphi_U)$ una carta alrededor de $p$ y $(V, \varphi_V)$ una carta alrededor de $f(p)$, donde $M$ es una variedad m-dimensional y $N$ es una variedad n-dimensional. Con estas cartas podemos dar una descripción coordenada de $f$, dada por $\tilde f = \varphi_V \circ f \circ \varphi_U^{-1}$. Digamos que $\bar \delta$ denota la representación coordenada de $\delta$ con la carta $(U, \varphi_U)$ y $\hat \gamma$ denota la representación coordenada de $\gamma$ con la carta $(V,\varphi_U)$. Las cartas inducen bases

de los espacios tangentes $T_pM$ y $T_{f(p)}N$, respectivamente. Queremos estudiar el mapeo $Df_p: T_pM \rightarrow T_{f(p)}N$ en términos de estas bases.

[Representación local de la diferencial] La matriz asociada a la representación de la transformación $Df_p: T_pM \rightarrow T_{f(p)}N$, en bases inducidas por las cartas, es $$ \left[ Df_p \right]_{\beta_1}^{\beta_2} = \begin{pmatrix} \frac{\partial \tilde f_1}{\partial x_1}(\bar p) & \cdots & \frac{\partial \tilde f_1}{\partial x_m}(\bar p) \\ \vdots & \ddots & \vdots \\ \frac{\partial \tilde f_n}{\partial x_1}(\bar p) & \cdots & \frac{\partial \tilde f_n}{\partial x_n}(\bar p) \end{pmatrix} $$ Es decir, si $v \in T_pM$ se puede expresar como $v = a^i \left( \partial x_i \right)_p$ entonces $$ Df_p(v) = a^i \frac{\partial \tilde f_i}{\partial x_j} (\partial x_j)_{f(p)} $$

En otras palabras la matriz de la diferencial $Df_p$ es la matriz jacobiana de la representación coordenada $\tilde f$ en el sentido clásico.

Para esto basta con calcular $Df_p$ en los vectores de la base $\beta_1 = \left\{ ( \partial x_i )_p \right\}_{i=1}^m$. Sea $w_i = Df_p(\partial x_i)$. Recordemos que $\partial x_i$ es la clase de curvas representada por la curva $\varphi_U^{-1}(\bar p + t e_i)$. Luego $w_i$ es la clase de curvas representada por $\gamma = f \circ \varphi_U ( \bar p + te_i)$. Puesto que la descomposición de este vector en la base $\beta_2 = \left\{ (\partial x_j)_{f(p)} \right\}_{j=1}^{n}$ está dada por las coordenadas de $\hat \gamma'(0)$ (véase esta ecuación), entonces hay que calcular el vector tangente de la representación coordenada de $\gamma$: $$ \begin{aligned} \hat \gamma'(0) & = \left( \varphi_V \circ \gamma \right)'(0) \\ & = \left( \varphi_V \circ f \circ \varphi_U^{-1}(\bar p + te_i) \right)'(0) \\ & = \left( \tilde f(\bar p + te_i) \right)'(0) \\ & = \left( \frac{\partial \tilde f_1}{\partial x_i}(\bar p), \cdots, \frac{\partial \tilde f_n}{\partial x_i}(\bar p) \right) \end{aligned} $$ y por lo tanto $$ Df_p( (\partial x_i)_p) = \frac{\partial \tilde f_j}{\partial x_i}(\bar p) \left( \partial x_j \right)_{f(p)} $$ De aquí se sigue la proposición.

Apéndices

El espacio tangente (curvas) es un espacio vectorial

Las operaciones de suma y multiplicación por escalares están bien definidas y definen una estructura de espacio vectorial en $T_pM$.
La demostración de este hecho no es esencial para lo que sigue, pero sirve para familiarizarse con esta noción de vector tangente. La definición que hemos dado de suma y producto por escalares depende de dos elecciones arbitrarias: depende de la elección de representante de la clase de equivalencia, y depende de las cartas usadas. Demostraremos que no depende de ninguna de las elecciones. Sean $(U, \varphi_U)$ y $(V, \varphi_V)$ dos cartas alrededor de $p$. Sean $\alpha_1,\alpha_2,\beta_1,\beta_2$ curvas diferenciables tales que $\alpha_i(0) = \beta_i(0) = p$ y $\alpha_i \sim_p \beta_i$ con $i=1,2$. Si definimos $$ \gamma_1 = \varphi_U^{-1}\left( \varphi_U \circ \alpha_1 + \varphi_U \circ \alpha_2 - \varphi_U(p) \right) \\ \gamma_2 = \varphi_V^{-1}\left( \varphi_V \circ \beta_1 + \varphi_V \circ \beta_2 - \varphi_V(p) \right) $$ entonces lo que queremos demostrar es que $\gamma_1 \sim_p \gamma_2$. Recordemos que demostrar $\gamma_1 \sim_p \gamma_2$ requiere demostrar la igualdad de vectores tangentes en una representación coordenada. Dado que basta con demostrarlo para una carta, podemos elegir la carta que prefiramos. Y en este caso nos conviene usar una de las cartas ya dadas. Usemos la siguiente notación: La representación de una curva $\nu$ con la carta $(U, \varphi_U)$ es $\bar \nu = \varphi_U \circ \nu$, y su representación con la carta $(V, \varphi_V)$ es $\hat \nu = \varphi_V \circ \nu$. Usando $(U, \varphi_U)$ para representar con coordenadas a $\gamma_1$ y $\gamma_2$ obtenemos $$ \bar \gamma_1 = \varphi_U \left( \varphi_{U}^{-1}\left( \bar \alpha_1 + \bar \alpha_2 - \varphi_U(p) \right) \right) = \bar \alpha_1 + \bar \alpha_2 - \varphi_U(p) \\ \bar \gamma_2 = \varphi_U\left( \varphi_V^{-1}(\hat \beta_1 + \hat \beta_2 - \varphi_V(p)) \right) = \Psi_{U}^V\left( \hat \beta_1 + \hat \beta_2 - \varphi_V(p) \right) $$ Por la regla de la cadena y la linealidad de la diferencial $$ \bar \gamma_2'(0) = D\Psi_U^V\left( \hat \beta_1'(0) + \hat \beta_2'(0) \right) = D\Psi_U^V\left( \hat \beta_1'(0) \right) + D\Psi_U^V(\hat \beta_2'(0)) $$ Sin embargo por la hipótesis $\alpha_i \sim_p \beta_i$ tenemos que $\hat \alpha_i'(0) = \hat \beta_i'(0) $, y además dado que $\hat \beta_i = \Psi_U^V \circ \alpha_i$, se sigue que $$ D\Psi_U^V(\hat \beta_i'(0)) = D\Psi_U^V\left( \hat \alpha_i'(0) \right) = \left( \Psi_U^V \circ \alpha_i \right)'(0) = \bar \alpha_i'(0) $$ Luego $$ \bar \gamma_2'(0) = D\Psi_U^V\left( \hat \beta_1'(0) \right) + D\Psi_U^V\left( \beta_2'(0) \right) = \bar \alpha_1'(0) + \bar \alpha_2'(0) = \bar \gamma_1'(0) $$ por lo que $\gamma_1 \sim_p \gamma_2$. La demostración de que $c\left[ \alpha \right]$ no depende ni de la carta ni del representante es casi idéntica y se deja para el lector. Demostrar que $T_pM$ es un espacio vectorial requiere verificar muchas propiedades. Seleccionamos algunas de modo un tanto arbitrario.
  1. El espacio tangente tiene un cero $0 \in T_pM$. Definimos el $0$ en $T_pM$ como la clase de la curva $0_p: \mathbb{R} \rightarrow M$ dada por $0_p(t) = p$. Dicha curva es diferenciable y satisface $0_p(0) = p$, por lo que define un vector tangente $[0_p] = 0$. Sea $\alpha: I \rightarrow M$ cualquier otra curva diferenciable con $\alpha(0) = p$. Queremos demostrar que $$ [\alpha] + 0 = \left[ \alpha \right] $$ Para esto hay que tomar una carta $(U,\varphi_U)$ y demostrar que $$ \left[ \alpha \right] + 0 = [\varphi_U^{-1}( \varphi_U \circ \alpha + \varphi_U \circ 0_p - \varphi_U(p))] = \left[ \alpha \right] $$ es decir si $\beta = \varphi_U^{-1}\left( \varphi_U \circ \alpha + \varphi_U \circ 0_p - \varphi_U(p) \right)$ entonces que $$ \beta \sim_p \alpha $$ De nuevo esto requiere demostrar que los vectores tangentes de alguna representación coordenada son iguales en $0$, y para esto tomaremos la misma carta $\left( U, \varphi_U \right)$ para representar a las curvas. $$ \bar \beta = \varphi_U \left( \varphi_{U}^{-1}\left( \bar \alpha + \bar 0_p - \varphi_U(p) \right) \right) = \bar \alpha + \varphi_U(0_p) - \varphi_U(p) = \bar \alpha $$ puesto que $\varphi_U(0_p(t))=p$ para todo $t \in \mathbb{R}$. Luego $\bar \beta'(0) = \bar \alpha'(0)$ y $\beta \sim_p \alpha$ y por lo tanto $\left[ \alpha \right] + 0_p = \left[ \alpha \right]$.
  2. Demostrar que todo vector tiene inverso aditivo: Sea $\left[ \alpha \right] \in T_pM$ un vector. Su representante es una curva diferenciable $\alpha: I \rightarrow M$ con $\alpha(0) = p$. Sea $\beta: I' \rightarrow M$ la curva definida por $\beta(t) = \alpha(-t)$. Dicha curva satisface $\beta(0) = \alpha(0) = p$ y es diferenciable. Afirmamos que $$ [\alpha] + [\beta] = 0 $$ De nuevo sea $(U,\varphi_U)$ cualquier carta alrededor de $p$, por lo que la suma $\left[ \alpha \right] + \left[ \beta \right]$ es la clase de equivalencia representada por la curva $$ \gamma = \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p \right) $$ Demostrar que $\left[ \alpha \right] + \left[ \beta \right] = 0$ es equivalente a demostrar que $\gamma \sim_p 0_p$. Con la misma carta $(U,\varphi_U)$, la representación coordenada de $\gamma$ bajo $\varphi_U$ es: $$ \bar \gamma = \bar \alpha + \bar \beta - \bar p $$ Notemos que $\bar \beta(t) = \varphi_U(\beta(t)) = \varphi_U(\alpha(-t)) = \bar \alpha(-t)$ y por lo tanto $\bar \beta'(0) = - \bar \alpha'(0)$, así $$ \bar \gamma'(0) = 0 = \bar 0_p'(0) $$ Luego $\gamma \sim_p 0_p$ y $[\alpha] + \left[ \beta \right] = 0$.
  3. Por último demostraremos que la multiplicación por escalares es distributiva. Sean $\left[ \alpha \right],\left[ \beta \right] \in T_pM$ y $c \in \mathbb{R}$. Queremos demostrar que $$ c\left( [\alpha] + \left[ \beta \right] \right) = c\left[ \alpha \right] + c\left[ \beta \right] $$ Sea $(U, \varphi_U)$ una carta alrededor de $p$. Luego las curvas $\left[ \alpha \right] + \left[ \beta \right]$, $c\left[ \alpha \right]$ y $c\left[ \beta \right]$ están representadas por $$ \left[ \alpha \right] + \left[ \beta \right] = \left[ \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p\right) \right] = \left[ \gamma \right] \\ c\left[ \alpha \right] = \left[ \varphi_U^{-1}\left( c \bar \alpha - (c-1) \bar p \right) \right] = \left[ \nu_1 \right] \\ c\left[ \beta \right] = \left[ \varphi_U^{-1}\left( c \bar \beta - (c-1) \bar p\right) \right] = \left[ \nu_2 \right] $$ Y por lo tanto las curvas $c\left( \left[ \alpha \right] + \left[ \beta \right] \right)$ y $c\left[ \alpha \right] + c\left[ \beta \right]$ están representadas por $$ c\left( \left[ \alpha \right] + \left[ \beta \right] \right) = c\left[ \gamma \right] = \left[ \varphi_{U}^{-1}\left( c \bar \gamma - (c-1)\bar p\right) \right] = \left[ \tau_1 \right] \\ c\left[ \alpha \right] + c\left[ \beta \right] = \left[ \nu_1 \right] + \left[ \nu_2 \right] = \left[ \varphi_U^{-1}\left( \bar \nu_1 + \bar \nu_2 - \bar p\right) \right] = \left[ \tau_2 \right] $$ Queremos demostrar que $\left[ \tau_1 \right] = \left[ \tau_2 \right]$, es decir $\tau_1 \sim_p \tau_2$. Para esto tomamos la misma carta $(U, \varphi_U)$ para representar con coordenadas a las curvas $\tau_i$. Noten que, por la definición de $\gamma$, $$ \begin{aligned} \bar \tau_1 &= c \varphi_U \circ \gamma - (c-1)\bar p\\ &= c \varphi_U \circ \varphi_U^{-1}\left( \bar \alpha + \bar \beta - \bar p\right) - (c-1)\bar p\\ &= c \bar \alpha + c \bar \beta -(2c-1)\bar p \end{aligned} $$ y, por las definiciones de $\nu_i$, $$ \begin{aligned} \bar \tau_2 &= \varphi_U \circ \nu_1 + \varphi_U \circ \nu_2 - \bar p \\ & =\varphi_U \circ \varphi_U^{-1}\left( c \bar \alpha - (c-1) \bar p \right) + \varphi_U \circ \varphi_U^{-1}\left( c \bar \beta - (c-1)\bar p \right) - \bar p\\ & = c \bar \alpha + c \bar \beta - 2(c-1) \bar p- \bar p\\ & = c \bar \alpha + c \bar \beta - (2c - 1)\bar p \end{aligned} $$ Luego $\bar \tau_1 = \bar \tau_2$, en particular $\bar \tau_1'(0) = \bar \tau_2'(0)$. Así $\tau_1 \sim_p \tau_2$ y por lo tanto $c(\left[ \alpha \right] + \left[ \beta \right]) = c\left[ \alpha \right] + c\left[ \beta \right]$.
Demuestra los axiomas de espacio vectorial que faltan.

Las funciones diferenciables de una variedad

En $\mathbb{R}^n$ existen diversas maneras de definir funciones apropiadas para diversas tareas. Sin embargo puede ser que nos encontremos muy limitados al tratar de encontrar funciones diferenciables en una variedad abstracta $M$.

Un método para definir funciones en $M$ podría ser como sigue: Tomen una carta $(U, \varphi_U)$ y usen las coordenadas para definir funciones en $U$. O dicho de otro modo si $f: \varphi_U \subset \mathbb{R}^n \rightarrow \mathbb{R}$ es cualquier función diferenciable entonces $\hat f = \varphi_U \circ f$ es una función diferenciable en $U$. Sin embargo esta receta sólo produce una función en $U$ que posiblemente sea difícil (si no es que imposible) extender diferenciablemente a una función en todo $M$.

Este problema es resuelto, parcialmente, por las funciones chipote.

Sean $U \subset V \subset \mathbb{R}^n$ conjuntos abiertos. Una función chipote para el par $(U,V)$ es una función diferenciable $h: \mathbb{R}^n \rightarrow \mathbb{R}$ tal que
  1. $h(x) = 1$ para todo $x \in U$.
  2. $h(x) = 0$ para todo $x \notin V$.
  3. $h(x) \geq 0$ para todo $x \in \mathbb{R}^n$.

Un resultado importante de la topología diferencial es el hecho de que siempre existen funciones chipote para cualquier par de abiertos $U \subset V \subset \mathbb{R}^n$ con $\overline{U} \subset V$. La demostración de este hecho está en las notas de particiones de la unidad. Así que, de ahora en adelante, simplemente vamos a aceptar la existencia de dichas funciones.

Estas funciones chipote nos ayudarán a extender funciones definidas localmente (en coordenadas) a toda la variedad.

Supongamos que estamos en una carta $(U,\varphi_U)$ y hemos elegido una función particular $f: \varphi_U(U) \rightarrow \mathbb{R}$ por que su comportamiento nos es favorable cerca del punto $x \in U$. Puesto que $U$ es un abierto existen $\varepsilon_1 < \varepsilon_2 < \varepsilon_3$ tales que $B_{\varepsilon_3}(x) \subset U$ y para los cuales podemos encontrar una función chipote $h$ para el par $(B_{\varepsilon_1}(x),B_{\varepsilon}(x))$. Notemos que la función $h$ es cero en una vecindad abierta de la frontera $\partial \varphi_U(U)$ (a saber $\mathbb{R}^n \setminus \overline{B_{\varepsilon_2}(x)}$) y $h=1$ en una vecindad de $x$. Luego la función $\tilde f = fh$ es una función definida en $\varphi_U(U)$ tal que $\tilde f = f$ en una vecindad abierta de $x$ y $\tilde f = 0$ en una vecindad abierta de $\partial \varphi_U(U)$. Luego si definimos $k: M \rightarrow \mathbb{R}$

entonces resulta que $k$ es una función diferenciable de $M$ cuya representación coordenada en la carta $(U, \varphi_U)$ satisface $\bar k = f$ en una vecindad de $x$.

Demuestra la afirmación anterior.

De este modo uno puede crear variedad de funciones con el comportamiento local que uno desee.